Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 23
Determine o volume do sólido dado.
23.
Abaixo do plano e acima da região limitada por e .
Passo 1
E aí, gente. Tudo belezinha?
Olha só, a questão quer o volume do sólido que está abaixo do plano e que está acima da região limitada por e por . Show?
O volume de um sólido qualquer pode ser limitado acima por uma superfície e abaixo pelo plano e é expressa através da seguinte integral dupla:
Em que D é a região limitada no plano em que devemos integrar a função.
Portanto, precisamos primeiro compreender como é a nossa região, se ela é do tipo I ou do tipo II. Para isto, começaremos esboçando-a.
Passo 2
Primeiramente, vamos esboçar a nossa região. Portanto,
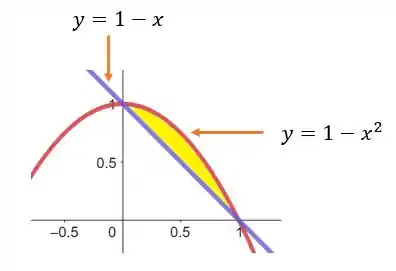
As duas curvas se intersectam nos pontos em que:
Elas se intersectam nos pontos e .
Em relação ao tipo da região, podemos escrevê-la tanto como região do tipo I quanto do tipo II. Portanto, vamos escolher arbitrariamente como sendo uma região do tipo I.
Explicando resumidamente, a região do Tipo I faz uma “sombra” no eixo , e nesse eixo existem uma região bem definida por pontos, que no nosso caso foi
Por isso nosso eixo não será definido por pontos, mas sim por funções, assim, ó:
Passo 3
Portanto, temos a seguinte integral:
Observe que a função foi obtida ao isolarmos a variável da equação do plano, já que estamos num plano , então .
Resolvemos a integral de dentro pra fora, ou seja, primeiro em relação a .
Organizando melhor, teremos:
Substituindo os limites de integração, teremos
E finalmente,
Agora integrando em relação a , vamos ter
Substituindo os limites, descobriremos o valor da nossa integral.