Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 67
Use a geometria ou simetria, ou ambas, para calcular a integral dupla
Passo 1
Faaaaala turma, tudo bem? Vamos nessa!!!
Usando de geometria ou simetria, ou ambas, precisamos calcular a integral dupla abaixo definida na região :
Por onde começamos essa?
Vamos começar por entender a nossa região D. Como ela é uma região retangular simétrica em torno do eixo e do eixo . Portanto, caso exista alguma função ímpar dentro da nossa integral, o seu resultado será 0.
O que é função ímpar? Uma função é ímpar quando:
Isto significa que os valores assumidos pela função serão simétricos tanto em relação ao eixo , quanto em relação ao eixo .
A integral de uma função impar em um intervalo simétrico vai ser zero, porque ao aplicar os limites de integração eles vão ser iguais porem com sinais diferentes, logo se cancelam.
Sabendo disso, foque na expressão dada e identifique se possui funções impares. Caso tiver, já sabemos que sua respota final vai ser zero.
Assim conseguimos simplificar a integral. Sua integral deve ficar com essa cara:
Muito parecida, com a integral do volume:
Logo, fazendo um gráfico da região podemos compreender e fazer semelhança com algum volume conhecido.
Agora ficou moleza ein!!! Bora lá resolver.
Passo 2
Vamos analisar nossa integral e identificar se algum termo tem a cara de uma função ímpar.
Lembre-se que uma função é impar se:
Analisando, temos duas possíveis funções impares:
Vamos verificar:
Logo, concluímos que realmente são impares.
Como nosso domínio é simétrico, o resultado da integral para essas funções será .
Portanto, a integral da nossa questão pode ser reescrita por:
Passo 3
Para podermos resolver a questão, precisamos identificar que sólido é este que estamos trabalhando, para assim relacionar a integral com o seu volume.
Observe a integral que obtemos no passo anterior:
Comparando com a integral do volume:
Vamos ter que é igual a:
Vamos usar o Geogebra para fazer um esboço dessa região. Para isso vamos assumir que .
Logo, vamos ter:
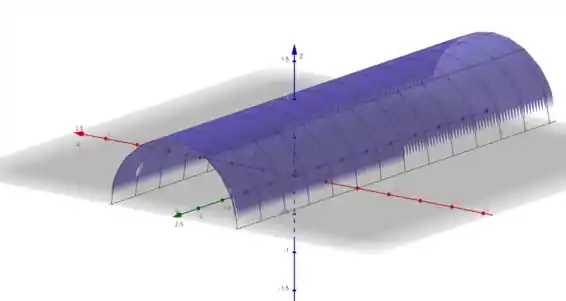
Observe essa figura, repare como ela é metade de um cilindro.
Passo 4
Já sabemos que nossa região é metade de um cilindro.
E avaliando a expressão de :
Chegamos à conclusão que o raio desse cilindro é a. Porque isso?
Pois,
Portanto, o volume de um cilindro é dado pela área da base (que está no plano ) vezes a altura, que está ao longo do eixo .
Onde,
Mas lembre-se que temos meio cilindro, logo nossa área deve ser dividida por .
Portanto,
Logo,