Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 11b
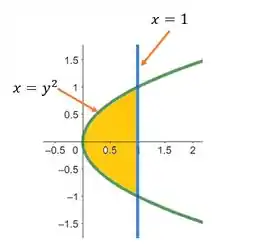
Desenhe um exemplo de uma região que seja
- Do tipo I, mas não do tipo II
- Do tipo II, mas não do tipo I
Passo 1
Fala aí, gente bonita!
Olha só, a questão quer, no item (b), um desenho de uma região que seja do Tipo II, e NÃO do tipo I. Show?
Precisaremos utilizar softwares para plotar as regiões. Mas antes disto, é preciso que realmente compreendamos o que é uma região do tipo 1 e uma do tipo 2.
Uma região do tipo 1 é uma região limitada acima e abaixo por uma curva, além disto, é limitada lateralmente por retas verticais. Portanto, o seu domínio é:
Já uma região do tipo 2 é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:
Resumindo, a região Tipo I faz uma “sombra” no eixo , e a região Tipo II faz uma “sombra” no eixo . Belê?
Passo 2
Para uma função do Tipo 2, mas não do Tipo 1, vamos escolher uma região limitada pelo seguinte domínio, chutando um exemplo pra vocês:
Como escolhemos uma região Tipo 2, observe que temos uma região bem delimitada no eixo , mas no eixo está delimitada por funções.
Portanto, seu gráfico será, segundo o software:
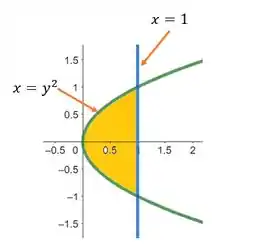
Em amarelo temos a nossa região em destaque!
Observe que temos no eixo uma região bem delimitada, com
Uma característica da nossa região Tipo II!
Resposta
