Expresse D como a região do tipo I e também como uma região do tipo II. Em seguida, calcule a integral dupla de duas maneiras.

13.

D é limitada pelas retas , , .

Temos um problema de integração em uma região geral. Precisamos entender que tipo de região estamos trabalhando para poder resolver a integral.

Uma região do tipo 1 é uma região limitada acima e abaixo por uma curva, além disto, é limitada lateralmente por retas verticais. Portanto, o seu domínio é:

Observe que no eixo temos pontos bem delimitados, enquanto no eixo temos funções que delimitam nossa região.

Já uma região do tipo 2 é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:

Ou seja, no eixo temos pontos bem definidos, mas no eixo não, pois são definidos por funções.

Vamos fazer a mágica acontecer!

Primeiramente, vamos esboçar a nossa região. Portanto,

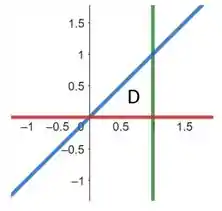
Em vermelho, está expressa a função , em verde, está e, em azul, .

Faremos primeiro uma região do Tipo I e resolver, certo?

Ela precisa ter bem definidos, então

Portanto, a nossa integral ficará assim:

Resolvendo-a, primeiro em relação a , teremos:

Agora em relação a ,

Vamos escrever a nossa região como uma região do tipo II. Portanto, ela tem pontos bem definidos no eixo . Assim,

Portanto, a nossa integral será:

Resolvendo-a, primeiro em relação a temos:

Integrando em relação a , teremos:

Uou! O mesmo resultado, independente do tipo que escolhermos. Sacou? 😉