Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 18
Calcule a integral dupla.
D é limitada por , , .
Passo 1
Temos um problema de integração em uma região geral. Nosso primeiro passo é esboçar a região e entender qual tipo de região estamos trabalhando.
Uma região do tipo 1 é uma região limitada acima e abaixo por uma curva, além disto, é limitada lateralmente por retas verticais. Portanto, o seu domínio é:
Já uma região do tipo 2 é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais. Portanto, temos o seguinte domínio:
Vamos então entender como a nossa região se comporta para podermos montar a integral.
Passo 2
Primeiramente, vamos esboçar a nossa região. Portanto,
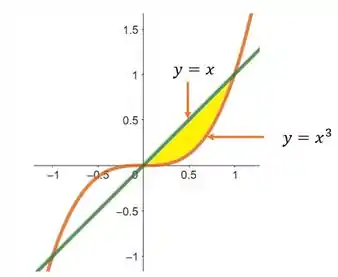
As duas curvas se intersectam nos pontos em que:
Como queremos uma região em que , os nossos pontos de interseção que limitam a região são os pontos e .
Neste caso, a nossa região se comporta tanto como uma do tipo I como do tipo II. Como não há restrição, escolheremos o primeiro caso para trabalhar.
Passo 3
Agora podemos começar a escrever a nossa região. Como a região do tipo I é limitada acima por uma curva e abaixo por outra, temos:
Já os limites laterais são . Portanto, temos a seguinte integral:
Resolvendo-a, temos: