Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.5 - Ex. 89a
Extensão contínua de para (0,)
a. Faça o gráfico de no intervalo 0
Passo 1
Fazendo o gráfico temos que:
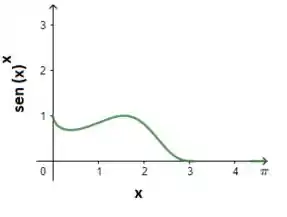
Para tornar a função contínua, o valor de deve ser nulo, onde x=0.
Resposta
Exercícios de Livros Relacionados
Se uma bola de metal de massa m for lançada na água e a força de resistência for proporcional ao quadrado da velocidade, então a distância que a bola percorreu até o instante t é dada por s ( t )= m c
Se um objeto de massa m é solto a partir do repouso, um modelo para sua velocidade v após t segundos, levando-se em conta a resistência do ar, é v = m g c( 1 - e - c t / m ) em que g é a aceleração da
Encontre o limite. Use a regra de L’Hospital quando for apropriado. Se existir um método mais elementar, use-o. Se a regra de L’Hospital não for aplicável, explique por quê. lim x → 0 + cos x 1 /
Ilustre a regra de L’Hospital fazendo o gráfico de f x / g ( x ) e f ' x / g ' ( x ) próximo de x = 0 , para ver que essas razões têm o mesmo limite quando x → 0 . Calcule também o valor exato do limi
Use gráficos para estimar o valor do limite. A seguir, use a regra de L’Hospital para encontrar o valor exato. lim x → 0 5 x - 4 x 3 x - 2 x