Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.5 - Ex. 89c
Extensão contínua de para (0,)
a. Voltando ao gráfico, calcule o valor máximo de em [0,]. Onde o valor max é assumido?
Passo 1
Fazendo o gráfico temos que:
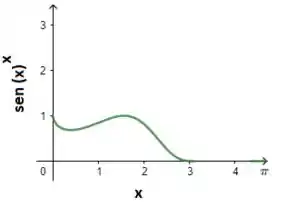
O valor máximo que será assumido será de 1.
Resposta
Exercícios de Livros Relacionados
Seja f x = e - 1 / x 2 , x ≠ 0 0 , x = 0 a) Use a definição de derivada para calcular f ' ( 0 ) .b) Mostre que f tem derivada de todas as ordens definidas em R . [Sugestão: Mostre primeiro por indução
Calculej) lim x → 0 - 1 - cos x 1 x
Calculel) lim x → 0 t g 3 x - s e n x s e n 3x
Calculem) lim x → 0 sec 3 x 1 - cos x
Calculeh) lim x → + ∞ x 2 + 1 1 ln x