Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 15

Se um extremo de um segmento de reta for o ponto (6,-2) e o ponto médio for (-1,5), ache as coordenados do outro extremo

Passo 1

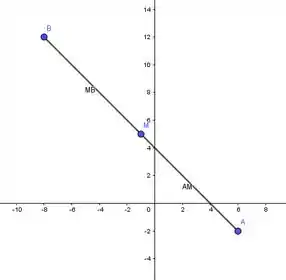
Chamaremos A(6,-2) e M(-1,5) queremos encontrar o ponto B ( x , y )   de forma que o segmento AM tenha a mesma medida do segmento MB, ou seja, M seja o ponto médio de AB. Por definição:

M = x + 6 2 , y + ( - 2 ) 2

Como, pelo enunciado, M(3,-1), temos

( - 1,5 ) = x + 6 2 , y + ( - 2 ) 2

Assim

x + 6 2 = - 1 ⇒

x + 6 = - 2 ⇒

x = - 2 - 6 ⇒

x = - 8

E também

y + ( - 2 ) 2 = 5 ⇒

y - 2 =   10 ⇒

y = 10 + 2 ⇒

y = 12

Resposta

Portanto o outro extremo do intervalo é o ponto B(-8,12)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com base na Figura 5.14, escrever equações paramétricas da reta:c) A e D .
A reta r passa pelo ponto A ( 4 , - 3 , - 2 ) e é paralela à reta s : x = 1 + 3 t y = 2 - 4 t z = 3 - t Se P ( m , n , - 5 ) ∈ r , determinar m e n .
Com base na Figura 5.14, escrever equações paramétricas da reta:f) B e D .
Com base na Figura 5.14, escrever equações paramétricas da reta:e) D e E .
Com base na Figura 5.14, escrever equações paramétricas da reta:b) C e D .