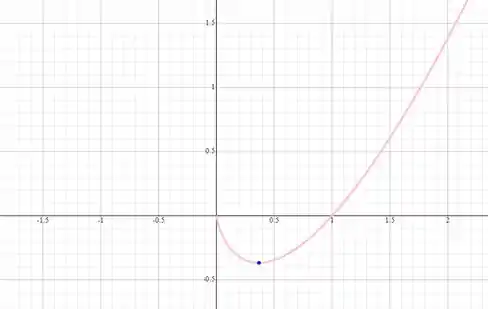
Um fabricante de geradores elétricos começa suas operações em 1º de janeiro de 1980. Durante o primeiro ano não houve vendas, pois a fábricaconcentrou esforços em pesquisas e no desenvolvimento do produto. Depois do primeiro ano as vendas cresceram constantemente, de acordo com a equação , onde é o número de anos durante os quais a fábrica esteve operando e é o número, expresso em milhões, do volume de vendas. (a) Faça um esboço do gráfico da equação.

O próximo passo é analisarmos as assíntotas horizontais e verticais. Vamos primeiro para as horizontais. O gráfico de uma função não terá assíntotas horizontais se ouLogo, não temos assíntotas horizontais.

Para a assíntota vertical, temos:

Como tempos uma indeterminação, devemos aplicar a regra de L’Hôpital e calcular o limite do quociente das derivadas:

Logo, não há assíntota vertical também.

Vamos encontrar agora os pontos críticos da função. Para isso, vamos derivar e igualar a zero.

Vamos verificar se existem pontos de inflexão e analisar se o ponto crítico que encontramos no passo anterior é um ponto de máximo ou mínimo. Para isso, vamos analisar a segunda derivada.

Como não há valor de que satisfaça essa equação, não temos ponto de inflexão. Se substituirmos o valor do ponto crítico na segunda derivada, podemos descobrir se tempos um ponto de máximo ou mínimo. Fazendo isso:

O valor encontrado para é positivo, o que implica dizer que é um ponto de mínimo local.

Vamos observar o comportamento da função .

Tendo essas informações podemos traçar nosso gráfico, com ponto mínimo em e interceptação no eixo x em .