Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.3 - Ex. 75
Suponha que a percentagem de lares dos Estados Unidos com acesso à Internet por meio de banda larga seja modelada por
em que é o número de anos decorridos depois de um levantamento inicial feito em 2007.
(a) Use um recurso computacional para traçar o gráfico de .
(b) Descreva o que acontece com a percentagem ao longo do tempo. Confira sua conclusão calculando .
(c) O que acontece com a taxa do crescimento dos lares com esse acesso ao longo do tempo? Confira sua conclusão traçando o gráfico de.
Passo 1
(a)
Usando recursos computacionais chegamos no seguinte gráfico:
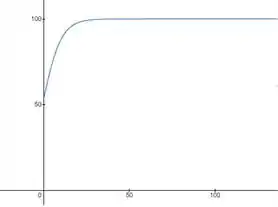
É importante lembrar que não faz tanto sentido pegar a parte do gráfico aonde , pois é uma quantidade de anos
Passo 2
(b)
Olhando para o gráfico conseguimos perceber que a porcentagem ao longo do tempo aumenta, com tendência de chegar a pra grandes períodos de tempo.
Para
Então:
De fato, para períodos muito grandes de tempo a porcentagem tende a .
Passo 3
(c)
Quanto mais lares tem acesso à internet, mais devagar cresce a porcentagem de lares com acesso, dado que a maioria já vai ter. Ou seja, pra períodos muito grandes essa taxa de crescimento tende a diminuir e ir a zero.
Achando
Usando a regra da derivação da divisão:
Se obtivermos o gráfico de :
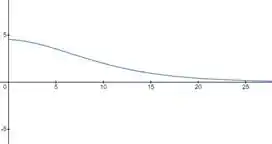
De fato, para períodos de tempo muito longos a taxa de crescimento tende a zero.
Resposta
Ei, a resposta está no passo a passo :)