Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 41
Um fabricante de latas quadradas sem tampas deseja usar pedaços de folhas-de-flandres com dimensões de 8 e 15 cm, cortando-se quadrados de lados iguais dos quatro cantos e dobrando os lados.
a): Se x cm for o comprimento do lado do quadrado a ser cortado, expresse o volume da caixa em como uma função de x
b): Qual o domínio da função ?
c): Prove que a função é contínua em seu domínio.
Passo 1
Letra a):
Para conseguirmos exprimir o volume como função do lado x, temos que ter em mente que, quando se corta os quadradinhos das pontas da folha e dobra, acontece algo deste tipo
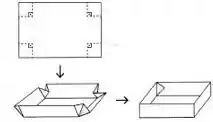
Assim, o lado de cada quadrado vai ser a altura da caixa e a base da caixa tem medidas (comprimento – 2x) e (largura-2x), onde o comprimento e a largura são 8cm e 15cm.
Assim, nosso volume será dado por
Passo 2
Letra b):
Considerando que nosso volume é um número não negativo e que eu não posso cortar um valor de x maior que 4cm, pois acabaria com o comprimento da folha, nosso domínio de V será
Passo 3
Letra c):
Como nossa função é polinomial de grau 3 (produto de 3 polinômios de grau 1), essa função sempre será contínua em todo seu domínio.