Faça alguns esboços para ilustrar os resultados do Exercício 80 e escreva um parágrafo dando uma explicação informal sobre o porquê de os resultados serem verdadeiros.
Passo 1
Comprovamos no exercício 80 que ao derivar uma função par, a função derivada vai se ímpar; a recíproca também vale.
Nisso, vamos pegar dois exemplos: os gráficos de uma função par e de uma função ímpar e os respectivos gráficos de suas derivadas.
A diferença entre as características de uma função ímpar e uma função par é a disposição dos gráficos com relação aos coordenados e . Enquanto a função par é simétrica em relação ao eixo , a função ímpar é antissimétrica ao mesmo eixo.
Vamos compará-los e ter uma noção visual melhor de como isso acontece!
Passo 2
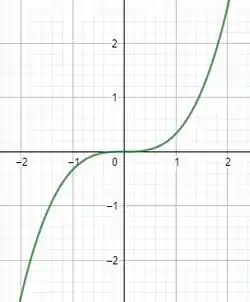
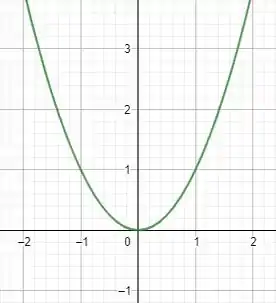
Repara as características com relação à simetria do gráfico frente aos eixos coordenados!
Passo 3
Fazemos o mesmo, agora com uma função par e sua derivada . Temos:
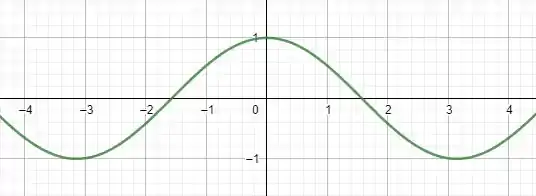
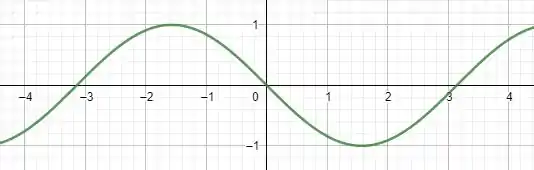
Mais uma vez, comparamos e vemos que, de novo, está obedecido o padrão de simetria pra funções pares e ímpares, de acordo com a paridade de cada função.
Resposta
Vide Passos 1, 2 e 3.