Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 11

Faça uma conjectura sobre o valor do limite

lim x → ∞ ⁡ x 2 2 x

Calculando a função f x = x 2 2 x para x = 0 ,   1 ,   2 ,   3 ,   4 ,   5 ,   6 ,   7 ,   8 ,   9 ,   10 ,   20 ,   50   e   100 . Então use o gráfico de f para comprovar sua conjectura.

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Boa galera, nesse exercício quando nos pedem uma conjectura estamos querendo inferir ou deduzir algo que é provável. Iremos nesse exercício tentar encontrar um valor para o limite proposto testando na função os valores pedidos. Após testar todos os valores, iremos tentar comprovar o valor que deduzimos graficamente.

Passo 2

Iremos substituir os valores propostos na nossa função f ( x )

Para f ( 0 ) , temos f 0 = 0

Para f ( 1 ) , temos f 1 = 0,5

Para f ( 2 ) , temos f 2 = 1

Para f ( 3 ) , temos f 3 = 1.125

Para f ( 4 ) , temos f 4 = 1

Para f ( 5 ) , temos f 5 = 0.78125

Para f ( 6 ) , temos f 6 = 0.5625

Para f ( 7 ) , temos f 7 = 0.3828125

Para f ( 8 ) , temos f 8 = 0.25

Para f ( 9 ) , temos f 9 = 0.158203125

Para f ( 10 ) , temos f 10 = 0.09765625

Para f ( 20 ) , temos f 20 = 0.00038147

Para f ( 50 ) , temos f 50 = 2.2204   x   10 - 12

Para f ( 100 ) , temos f 110 = 7.8886   x   10 - 27

Conforme os valores de x aumentam, o valor da função tende a zero. Dessa forma, deduzimos que

lim x → ∞ ⁡ x 2 2 x = 0

Passo 3

Gerando o gráfico com o auxílio do GeoGebra:

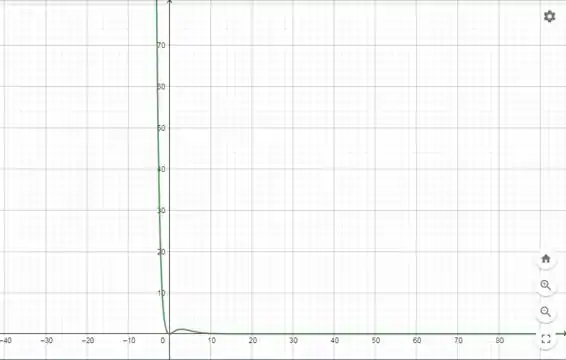
Olhando para o gráfico, podemos ver que conforme o valor de x aumenta, o valor de y tende a 0 . Dessa forma, pode se concluir que

lim x → ∞ ⁡ x 2 2 x = 0

Resposta

lim x → ∞ ⁡ x 2 2 x = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize as definições de limite à direita e à esquerda para provar o limite abaixo lim x → 0 - ⁡ x | x | = - 1
Suponha que f seja uma função ímpar de x . Saber que lim x → 0 + ⁡ f x = 3 diz algo sobre lim x → 0 - ⁡ f x ? Justifique sua resposta.
Suponha que f seja uma função par de x . Saber que lim x → 2 - ⁡ f x = 7 diz algo sobre lim x → - 2 - ⁡ f x ou lim x → - 2 + ⁡ f x ? Justifique sua resposta.
Utilize as definições de limite à direita e à esquerda para provar o limite abaixo lim x → 2 + ⁡ x - 2 | x - 2 | = 1
Uma vez que conheça lim x → a + ⁡ f ( x ) e lim x → a - ⁡ f ( x ) em um ponto interior do domínio de f , você poderá determinar lim x → a ⁡ f ( x ) ? Justifique sua resposta