Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.1 - Ex. 21

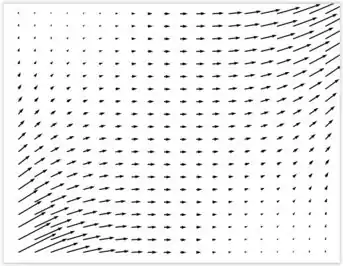
Determine o campo vetorial gradiente f .

f x , y = x e x y

Passo 1

Fala pessoal , para determinarmos o campo vetorial, devemos tomar o gradiente da função f , ou seja,

F → = ∇ f

Lembrando que o gradiente de uma função é definido por um vetor, cujas as componentes são as derivadas parciais em cada direção, ou seja

F → = ∂ f d x ,   ∂ f d y

Beleza, então para resolvermos essa questão precisamos achar as derivadas parciais e depois criar o campo vetorial , ok?

Passo 2

Vamos tomar inicialmente a derivada de f na direção x .

∂ f d x = ∂ x e x y d x =   e x y + y x e x y = e x y ⋅ ( 1 + x y )

E na direção y temos

∂ f d y = ∂ x e x y d y = 0 + x 2 e x y = x 2 e x y

Desta forma escrevemos que

F → = e x y ⋅ 1 + x y , x 2 e x y = e x y 1 + x y , x 2

F → = e x y + e x y x y , e x y x 2

Passo 3

Beleza, agora que temos o vetor gradiente definido, como podemos montar o gráfico?

Para cada ponto teremos um vetor, representado por uma seta. Lembrando que , um vetor irá ter um módulo, que nesse caso será a magnitude , ou seja, a maior variação de valor que a função terá naquele ponto. Além da direção e sentido que serão determinadas pelos pontos ( x , y ) .

Uma forma legal para começar é escolher pontos aleatórios e substituí-los nas componentes que você achou anteriormente.

Vamos ver um exemplo :

Primeiro passo é escolher um ponto qualquer que seja fácil de visualizar.Esse ponto será chamado de ponto inicial do vetor, e mais para frente isso fará mais sentido.

                  F → = 1,1

Se observarmos esse ponto em um gráfico ele será representado da seguinte forma :

Após escolhermos o ponto, substituiremos na componente que achamos anteriormente:

F → = e x y + e x y x y , e x y x 2

Substituindo :

F → = e 1.1 + e 1.1 1.1 , e 1.1 . 1 2

Agora vamos multiplicar esses valores:

F → = e 1 + e 1 . 1 , e 1 . ( 1.1 )

F → = e + e , e

F → = 2 e , e

F → = 5.4365 , 2.7182

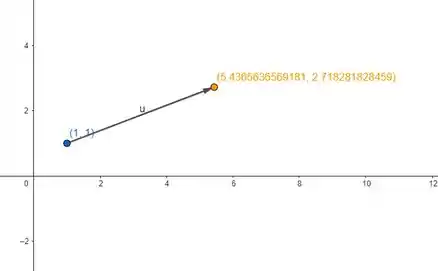
Esse ponto será chamado de ponto final do vetor. Você lembra do ponto de origem que escolhemos lá no início ? Então, ligando o ponto de origem com o ponto final nós vamos desenhar o vetor gradiente para um ponto. O gráfico abaixo vai te ajudar a visualizar melhor:

Passo 4

Beleza, mas e o resto dos vetores, será que você vai precisar fazer muitos pontos para construir o campo vetorial?

Bom , a resposta é não.

Vamos dar uma olhadinha nas componentes do vetor gradiente.

F → = e x y + e x y x y , e x y x 2

É possível observar que ambas as coordenadas ( x , y )   terão o número de euler   ( e ) , que é um número maior que zero, ou seja, sempre positivo.

A partir dessa definição, podemos deduzir que os vetores sempre serão crescentes.

Outro ponto importante é , se mantermos o ponto y constante e irmos aumentando gradativamente o ponto x , podemos observar que a inclinação do vetor irá diminuir.

E se mantermos o ponto x constante e aumentarmos o ponto y iremos observar que o comprimento do vetor será cada vez menor. Como mostra o gráfico abaixo:

Resposta

F → = e x y ⋅ 1 + x y , x 2 e x y = e x y 1 + x y , x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o campo vetorial gradiente ∇ f de f e o esboce. f x ,y = x 2 - y
Trace o campo vetorial gradiente de f e o mapa de contorno de f . Explique como eles estão relacionados. f x ,y = sen ⁡ x + sen ⁡ y
Seja F x = r 2 - 2 r x , onde x = x ,y e r = x . Use um SCA para traçar esse campo vetorial em vários domínios, até conseguir visualizar o que ocorre. Descreva a aparência do desenho e explique-o, det
Determine o campo vetorial gradiente de f .f (x , y , z) = sqrt(x^2 + y^2 + z^2)
Faça a correspondência entre o campo vetorial F → em R 3 e a figura rotulada de I - I V . Justifique suas escolhas. F → x , y , z = x i → + y j → + z k →