Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 17
Faça a correspondência entre o campo vetorial em e a figura rotulada de . Justifique suas escolhas.
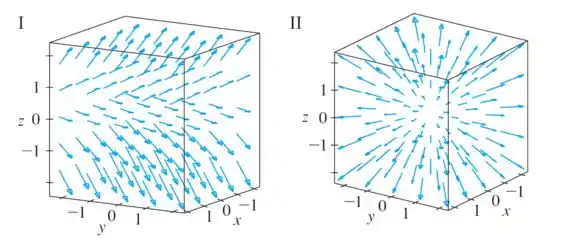
Passo 1
Falaa, galera, tudo bem?
Essa questão pede pra gente descobrir qual dessas quatro imagens representa o campo
Pra isso, vamos analisar essa expressão, pra entender como são os vetores desse campo, a depender do ponto que estamos.
Assim, conseguimos relacionar qual das imagens representa nosso campo.
Passo 2
Como esses versores representam as três coordenadas do vetor, temos que:
Daqui conseguimos ver que a terceira coordenada é constante e igual a , o que indica que todos os vetores estão apontando pra cima!
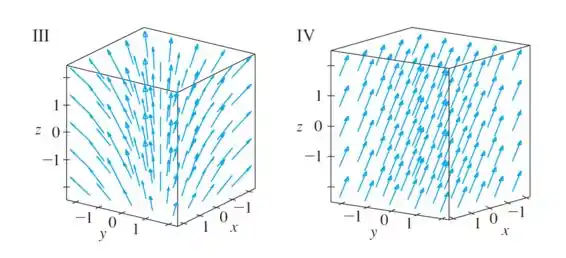
Temos duas figuras que isso acontece, a e a :
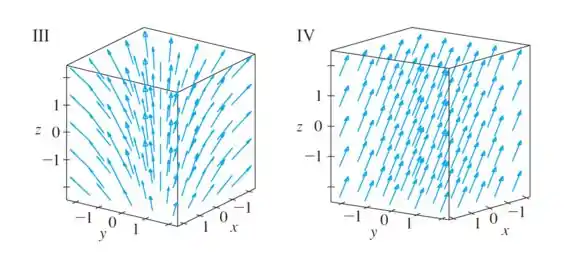
Só que percebe que a figura representa um campo constante, já que todos os vetores são iguais (têm mesmo tamanho e apontam pra mesma direção).
Já a figura , apesar de todos apontarem pra cima, são vetores diferentes, que mudam conforme e , que é o que acontece com o nosso campo.
Então a figura que representa nosso campo é a