Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 6

6. Calcule o trabalho realizado pelo campo de força

F x , y , z = y 2 ,   z 2 , x ²

Ao longo da curva obtida como interseção da esfera

x 2 + y 2 + z 2 = a 2

Com o cilindro

x 2 + y 2 = a x

Onde z ≥ 0   ,   a ≥ 0 . A curva é percorrida no sentido anti-horario quando vista do plano xy

Passo 1

Oii, estamos avançando e agora temos que traduzir os problemas. Ao pedir o trabalho de algo temos que lembrar que

T = F ⋅ ∆ r

Ou seja, força vezes distância. Se formos colocar em notação de integral seria

∫ c F ⋅ d r

Que é nossa integral de linha clássica.

Passo 2

No nosso caso temos que percorrer o seguinte percurso: curva obtida como interseção da esfera

x 2 + y 2 + z 2 = a 2

Com o cilindro

x 2 + y 2 = a x

Onde z ≥ 0   ,   a ≥ 0 . Esse tipo de curva da um trabalhinho para resolver a interseção. Como temos que procurar uma parametrização para essa curva. Vamos primeiro pensar no cilindro e completar quadrados

x 2 + y 2 = a x

x 2 - a x + a 2 2 - a 2 2 + y 2 = 0

x - a 2 2 + y 2 = a 2 2  

Logo uma parametrização mais apropriada seria usar coordenadas polares

cos 2 ⁡ t + sen 2 ⁡ t = 1

x - a 2 2 + y 2 = a 2 2  

Isso faz com que nossa parametrização fica

x = a 2 cos ⁡ t + a 2

y = a 2 sen ⁡ t  

Agora basta acharmos z. podemos fazer um sistema

x 2 + y 2 + z 2 = a 2

x 2 + y 2 = a x

E achar a seguinte relação

a x + z 2 = a 2

z = a 2 - a x

Oque nas nossas novas coordenadas fica

z = a 2 - a a 2 cos ⁡ t + a 2

z = a 2 1 - cos ⁡ t 2 - 1 2

z = a 1 2 - cos ⁡ t 2

Show!!! Nossa curva então tem essa cara

γ t = a cos ⁡ t 2 + 1 2 , sen ⁡ t 2 , 1 2 - cos ⁡ t 2  

É uma parametrização estranha. Mas se olharmos o gráfico ela funciona

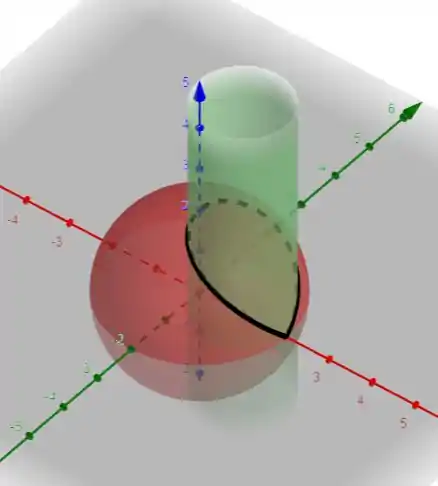
Onde a curva Preta é nossa interseção entre o cilindro e a esfera.

Passo 3

Entao nossa parametrização é

γ t = a cos ⁡ t 2 + 1 2 , sen ⁡ t 2 , 1 2 - cos ⁡ t 2  

γ ' t = a - sen ⁡ t 2 , cos ⁡ t 2 , sen ⁡ t 2 2 1 2 - cos ⁡ t 2  

t ∈ 0,2 π

Vamos parametrização nossa função Força!!!

F x , y , z = y 2 ,   z 2 , x ²

F γ t = a 2 4 sen 2 ⁡ t ,   a 2 1 2 - cos ⁡ t 2 ,   a 2 cos ⁡ t 2 + 1 2

Passo 4

Bora integrar !!!

∫ C F ⋅ d   r → =   ∫ t 0 t 1 F γ ( t ) ⋅ γ ' t d t

=   ∫ 0 2 π a 2 4 sen 2 ⁡ t ,   a 2 1 2 - cos ⁡ t 2 ,   a 2 cos ⁡ t 2 + 1 2 ⋅ a - sen ⁡ t 2 , cos ⁡ t 2 , sen ⁡ t 2 2 1 2 - cos ⁡ t 2   d t

= a 3 ∫ 0 2 π - 1 8 sen 3 ⁡ t + cos ⁡ t 4 - cos 2 ⁡ t 4 + sen ⁡ t cos ⁡ t 8 1 2 - cos ⁡ t 2 + sen ⁡ t 8 1 2 - cos ⁡ t 2 d t

Uma coisa que pode facilitar nossa integração é que funções sen k ⁡ t e cos k ⁡ t se k for impar e integrarmos no intervalo 0,2 π tem como resultado zero. Logo podemos excluir o termos

- 1 8 sen 3 ⁡ t , + cos ⁡ t 4

O que resume nossa integral a

a 3 ∫ 0 2 π - cos 2 ⁡ t 4 + sen ⁡ t cos ⁡ t 8 1 2 - cos ⁡ t 2 + sen ⁡ t 8 1 2 - cos ⁡ t 2 d t

Vamos usar uma identidade trigonométrica

cos 2 ⁡ t = 1 2 + cos ⁡ 2 t 2

Com isso vamos facilitar nossa integração

a 3 ∫ 0 2 π - 1 4 1 2 + cos ⁡ 2 t 2 + sen ⁡ t cos ⁡ t 8 1 2 - cos ⁡ t 2 + sen ⁡ t 8 1 2 - cos ⁡ t 2 d t

= a 3 - t 8 - 1 8 sen ⁡ 2 t 2 0 2 π + ∫ 0 2 π sen ⁡ t cos ⁡ t 8 1 2 - cos ⁡ t 2 + sen ⁡ t 8 1 2 - cos ⁡ t 2 d t

= a 3 - π 4 - 1 8 0 - 0 + ∫ 0 2 π sen ⁡ t ( cos ⁡ t + 1 ) 8 1 2 - cos ⁡ t 2 d t

= a 3 - π 4 + ∫ 0 2 π sen ⁡ t ( cos ⁡ t + 1 ) 8 1 2 - cos ⁡ t 2 d t

Se você tem alguma intuição que essa integral vai ser nula. Pode comemorar que sim, ela vai se anular. Só vamos ter um bom trabalho para explicar isso. Vamos usar Integração por Partes.

( u v ) ' = u ' v + u v '

∫ ( u v ) ' d t = ∫ u ' v d t + ∫ u v ' d t

u v = ∫ u ' v d t + ∫ u v ' d t  

O que vamos fazer é dizer que

v ' = sen ⁡ t 8 1 2 - cos ⁡ t 2  

  u = cos ⁡ t + 1  

E assim nossa relação fica

∫ u v ' d t =   u v -   ∫ u ' v d t

Logo temos que primeiro integrar v '

∫ 0 2 π sen ⁡ t 8 1 2 - cos ⁡ t 2 d t

Que se resolve por substituição

u =   1 2 - cos ⁡ t 2

d u = 1 2 sen ⁡ t d t

Entao ficamos com

∫ 0 2 π sen ⁡ t 8 1 2 - cos ⁡ t 2 d t → 1 4 ∫ 1 u d u

= 1 2 u 1 2

Vamos voltar de u → t

1 2 u 1 2 → 1 2 1 2 - cos ⁡ t 2 1 / 2 0 2 π

= 1 2 1 2 - 1 2 1 2 - 1 2 - 1 2 1 2

= 0

Ufaaa!!!! Uma integração a menos . Vamos voltar a nossa integração principal

∫ u v ' d t =   u v -   ∫ u ' v d t

∫ 0 2 π sen ⁡ t ( cos ⁡ t + 1 ) 8 1 2 - cos ⁡ t 2 d t = cos ⁡ t + 1   0 -   ∫ 0 2 π - sen ⁡ t 0 d t

= 0

Com isso se voltarmos a nossa relação lá de cima teremos

= a 3 - π 4 + ∫ 0 2 π sen ⁡ t ( cos ⁡ t + 1 ) 8 1 2 - cos ⁡ t 2 d t

= a 3 - π 4 + 0

= - a 3 π 4

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

∫ c F ⋅ d r   = - a 3 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça uma correspondência entre as funções f e os desenhos de seus campos vetoriais gradientes (rotulados de I - I V ). Justifique suas escolhas. f x ,y = x ( x + y )
Faça uma correspondência entre as funções f e os desenhos de seus campos vetoriais gradientes (rotulados de I - I V ). Justifique suas escolhas. f x ,y = x + y 2
No instante t = 1 , uma partícula está localizada na posição 1 ,3 . Se ela se move em um campo de velocidade F x , y = x y - 2 ,y 2 - 10 encontre sua posição aproximada no instante t = 1,05 .
(a) Esboce o campo vetorial F x ,y = i + xj e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?(b) Se as equações paramétricas das linhas de escoamento são x =
Uma partícula se move em um campo de velocidade V x , y = x 2 ,y + y 2 . Se ela está na posição 2 ,1 no instante t = 3 , estime sua posição no instante t = 3,01 .