Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 61
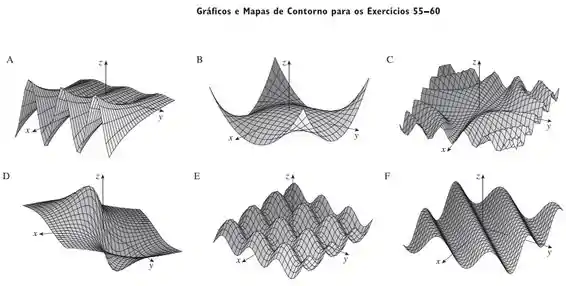
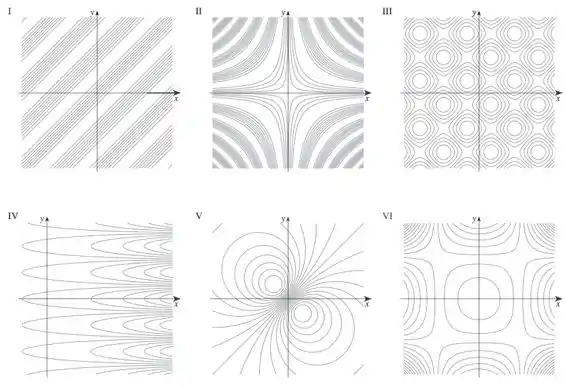
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha.
Passo 1
Falaaa, meu parceiro. É o seguinte, vamos resolver essa atividade juntos e você vai sair daqui sabendo tudo.
Temos então a função:
E queremos relacionar qual o gráfico dessa função e qual sua curva de nível, dentre as várias opções que nos foram dadas.
Para escolhermos corretamente qual o gráfico tridimensional dessa função, deveremos analisar o comportamento da mesma em determinados pontos, isso nos dará algumas dicas.
O interessante aqui é a que a função seno é limitada,
Então veremos uma oscilação dentro desse intervalo em todas as direções. Devemos ter em mente também que temos aqui um produto entre duas variáveis, e que ambas podem ser positivas, ambas podem ser negativas, ou cada uma pode ter um sinal oposto.
Isso influenciará, pois, a função seno tem o seguinte comportamento:
Passo 2
(a) Não é tão simples relacionar de cara a função ao seu gráfico, mas se pensarmos no seno, temos uma função assimétrica.
Olhando para a multiplicação no plano onde quando temos sinais iguais a multiplicação é positiva e com sinais diferentes, temos sinal negativo.
A função seno, partindo do argumento para a parte positiva, aumentea e depois oscila e na parte negativa ela diminui e segue o mesmo padrão da positiva, simetricamente oposta.
Além disso, quando uma das variáveis é a função zera e quanto mais longe da origem, com nenhuma variável zerada, temos uma frequência maior para o argumento do seno, diminuindo o comprimento da onda do seno.
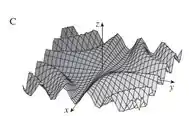
O gráfico que segue esse padrão é o gráfico C.
Passo 3
(b) Analisando as curvas de nível, manipulando a equação, se pegarmos sendo uma constante qualquer
Já que é constante, também é constante
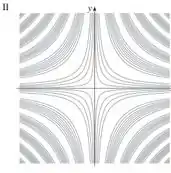
Essa é uma função de hipérbole, o gráfico que tem esse comportamento é o II.
Resposta
- C
- II