Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 40
Faça o mapa de contorno da função mostrando várias curvas de nível.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos desenhar o mapa de contorno da função mostrando várias curvas de nível.
Para isso, precisamos chegar à função das curvas de nível fazendo , onde é uma constante.
Depois vamos variando (dando valores) para representar algumas curvas de nível no mapa.
Agora bora lá!! 😉
Passo 2
Primeiro vamos dar uma organizada para isolar uma variável
Temos que, pelo que vimos no passo 1:
Aplicando o logaritmo natural nos dois lados , temos:
Sabemos que , logo:
Isolando :
Trata-se da equação da reta ( com e .
ATENÇÃO: como está no denominador, !!
Variando , chega-se ao seguinte mapa de contorno:
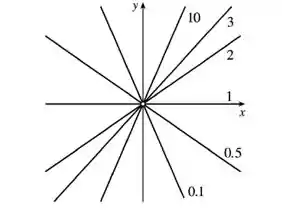
Vale notar o ponto em aberto no gráfico (correspondente a ).
Para ficar melhor a visualização, veja o gráfico da nossa função:
Perceba que quanto mais a curva chega perto do eixo , maior o valor da função. 😉
Resposta
