Faça uma correspondente entre a função e seu gráfico (identificado por I–VI). Justifique sua escolha.
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Falaeee, belezinha?? Bom... a questão é bem direta... O enunciado nos deu as seguintes equações:
(a)
(b)
(c)
(d)
(e)
(f)
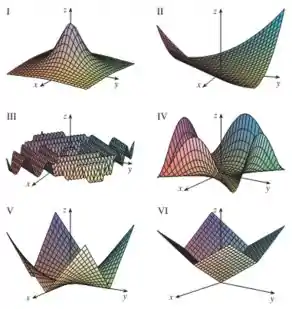
E também nos deu os gráficos delas... mas eles não estão em ordem:
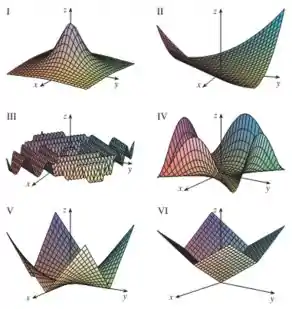
Assim, a nossa tarefa aqui é relacionar cada gráfico com cada equação!! 😉
Para resolver essa questão, vamos olhar os cortes que as funções deixam nos planos e .
E vamos analisar cada função em separado.
Lembre-se também que precisamos saber que a função está na forma:
Passo 2
Na letra (a), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
Perceba que temos um módulos simples em cada uma.
Lembra que o gráfico do módulo é um ? Pois é!!
Assim, só pode ser o gráfico VI:
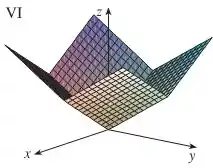
Agora vamos fazer a mesma coisa análise para as outras alternativas:
Passo 3
Na letra (b), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
Como na letra (a), o nosso gráfico também tem características de de uma função modular (descrevendo um ).
Mas aqui quando zeramos uma das variáveis, a função toca no zero dos respectivos eixos.
Assim, só pode ser o gráfico V:
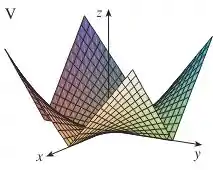
Passo 4
Na letra (c), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
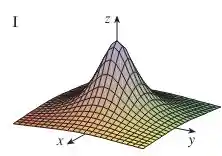
Perceba que quando e se aproximam da origem, o valor de é máximo.
Assim, só pode ser o gráfico I:
Passo 5
Na letra (d), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
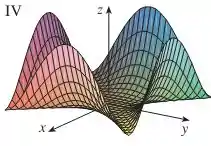
Note que em (plano ):
Logo, só pode ser o gráfico IV:
Passo 6
Na letra (e), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
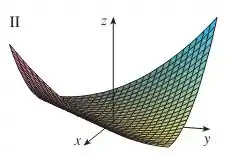
Note que em (plano ), temos:
Só pode ser o gráfico II:
Passo 7
Na letra (f), temos:
Agora vamos olhar os planos dimensionais fazendo uma variável ir para zero:
(Plano )
(Plano )
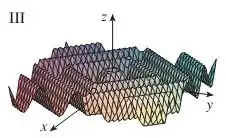
O único gráfico que tem a aparência de senóide (“ondas”) é o III:
Resposta
(a) VI
(b) V
(c) I
(d) IV
(e) II
(f) III