Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 17
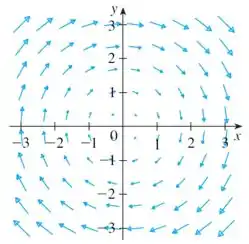
Seja o campo vetorial mostrado na figura.
- Se é o segmento de reta vertical de a , determine se é positivo, negativo ou zero.
- Se é o círculo de raio e centrado na origem, percorrido no sentido anti-horário, determine se é positivo, negativo ou zero.
Passo 1
Faala, pessoal!
Nessa questão temos um campo vetorial definido pela figura, e queremos saber se duas integrais de linha desse campo são positivas, negativas ou zero.
Pra isso, a gente tem que ter em mente essas situações:
- Se a curva estiver sendo percorrida toda no mesmo sentido do campo, o trabalho (e, portanto, a integral de linha sobre ela) é positiva!
- Se estiver sendo percorrida no sentido contrário, é negativa!
- Se em alguns pontos estiver no mesmo sentido e em outros no sentido contrário, pode ser que eles se cancelem (e aí seria zero), ou se os que apontam em um sentido superarem (em quantidade ou em tamanho) o do outro sentido, eles “ganham”.
Vamos desenhar cada uma das curvar em cima do nosso desenho do campo pra analisar isso e tirar as nossas conclusões!
Passo 2
(a)
Na letra (a), a nossa curva é o segmento de reta vertical de a . Então fica assim:
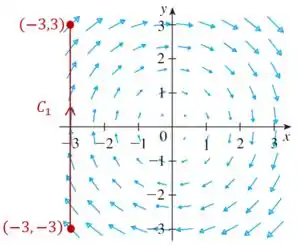
Percebe que nesse intervalo da curva todos os vetores do campo estão apontando pra cima (sentido positivo de ), e é a mesma direção que a curva é percorrida.
Ou seja, apesar de não conseguirmos afirmar o valor:
Passo 3
(b)
Já a curva é o círculo de raio e centrado na origem, percorrido no sentido anti-horário. No desenho, fica assim:
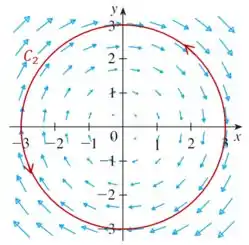
Enquanto os vetores do campo estão apontando sempre no sentido horário, a curva é percorrida no sentido anti-horário. Então:
Resposta
- Positivo
- Negativo