Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 2b
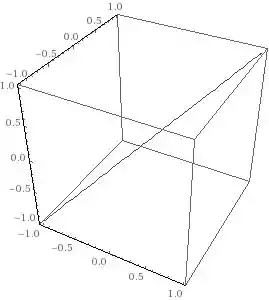
Faça um esboço das curvas definidas pelas seguintes funções vetoriais:
Passo 1
Esse item nos fornece a seguinte função vetorial:
Vamos começar substituindo o parâmetro das equações paramétricas por alguns valores do intervalo :
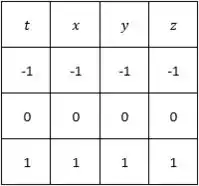
Resposta
Esboçando a curva a partir dos pontos presentes na tabela chegaremos em algo parecido com isso:
Exercícios de Livros Relacionados
Verificar que a curva r → t = t c o s ti → + t s e n t j → + tk → , t ≥ 0 Está sobre um cone.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos t ,1 + 4 s e n t , t ∈ 0 ,2 π
Uma hipociclóide é a curva traçada por um ponto P sobre uma circunferência de raio b que gira dentro de uma circunferência fixa de raio a , a ≥ b . Suponha que a origem é o centro da circunferência fi
Considere a curva definida por σ t = 1 + 2 ln 1 + t , 1 + 1 + t 2 ,t- 1 Determine uma equação da reta tangente à curva no ponto 1,2
Considere a curva definida por σ t = 1 + 2 ln 1 + t , 1 + 1 + t 2 ,t- 1 b) Dê uma equação cartesiana da curvac) Esboce a curva