Faça o esboço da equação
Passo 1
Para esse esboço, vamos fazendo passo a passo, da equação mais básica até a da que a questão pede.
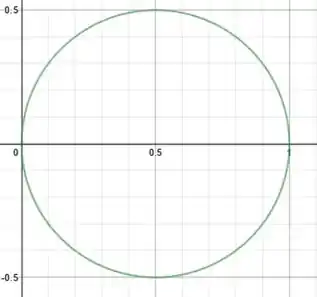
Passo 2
Ao passarmos a raiz para o outro lado, a equação fica:
E isso significa que o nosso cosseno vai ser atenuado por causa da raíz quadrada, além de aumentar 4 vezes o seu tamanho (isso por causa do 4 multiplicando tudo antes).
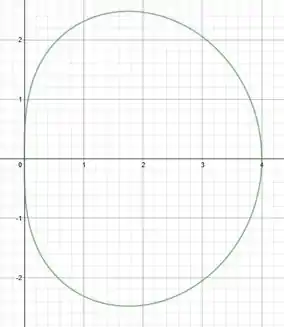
E tá pronto o sorvetinho!!
Resposta
Ei, a resposta está no passo a passo :)