Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 33a
Faça um esboço do gráfico de:
Passo 1
A princípio parece bem estranho né? Mas vamos digerir essa equação com calma. A gente ta trabalhando com uma coisa chamada espiral hiperbólica (inversa da espiral de Arquimedes). Ela começa com uma assíntota de y=a e vai ficando cada vez menor, igual um caracol.
Passo 2
Sabendo disso, temos a nossa equação
Olhando pra ela, é fácil saber que o nosso a corresponde a 3, logo, a nossa assíntota quando tende ao infinito, vai se tornando 3.
Portanto, fica fácil desenhar a nossa espiral.
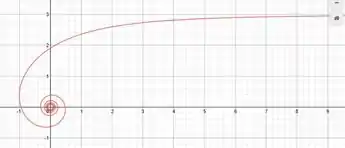
Resposta
Exercícios de Livros Relacionados
Escreva a equação (a) em coordenadas cilíndricas e (b) em coordenadas esféricas. x 2 + y 2 + z 2 + 2 z = 0
Esboce o desenho do sólido descrito pelas desigualdades 0 ≤ ∅ ≤ π 3 , ρ ≤ 2
Utilize um dispositivo gráfico para desenhar o sólido envolvido pelos paraboloides z = x 2 + y ² ² e z = 5 - x 2 - y ² ².
(a) Ache as inequações que descrevem uma bola oca com diâmetro de 30 cm e espessura de 0,5 cm. Explique como você posicionou o sistema de coordenadas que escolheu.(b) Suponha que a bola seja cortada p
Plote o ponto cujas coordenadas polares são dadas. Então encontre as coordendas cartesianas do ponto.a) 2 , 2 π 3 b) 4 ,3 π c) - 2 ,- 5 π 6