Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.1 - Ex. 49
Faça um esboço do gráfico da função dada.
Passo 1
A questão pede para esboçarmos o gráfico da função . Para esboçarmos gráficos de funções trigonométricas inversas, uma dica muito importante é ver o comportamento da função trigonométrica correspondente.
Invertendo
Assim, a inversa de é , onde
Para que a cotangente seja invertível, devemos ter
Neste intervalo, o gráfico de é:
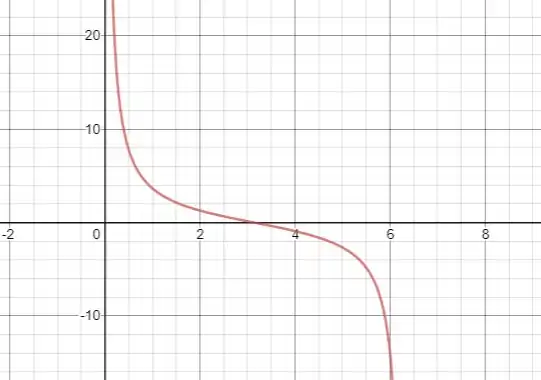
Passo 2
Para o gráfico de , basta inverter domínio com imagem e lembrar que os gráficos de e de devem ser simétricos com relação a reta :
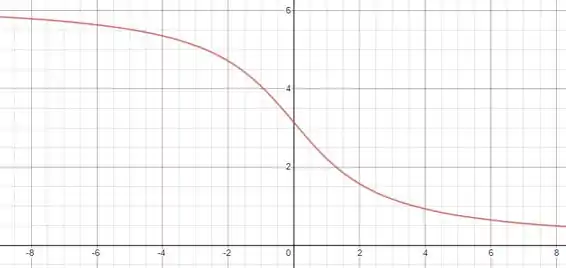
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
Encontre uma formula explicita para f - 1 e use para traçar um gráfico f - 1 ,f e a linha y = x na mesma tela. Para checar se está correto, veja se os gráficos de f - 1ef são refletidos pela linha. f
Dada a função y = f x = x 1 + x 2 definida para todo x real, demonstrar que a sua inversa é a função x = g y = y 1 - y 2 definida para y1 .
Em cada um dos exercícios determine a fórmula da função inversa. Fazer os gráficos da função dada e de sua inversa. hy = x 2 - 4 ,x ≤ 0
Mostre que y = f x = x + 2 2 x - 1 coincide com a sua inversa, isto é, x = f ( y ) ou f f x = x .
Seja f (x) = {[[x , s e x1],[x^2 , s e 1 = x = 9],[27 sqrt(x) , s e x9]]) . Verifique que f tem uma inversa e encontre f^(- 1) ( x ) .