Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.8 - Ex. 5
Descreva em palavras a superfície cuja equação é dada.
Passo 1
E aí, pessoal! Tranquilidade?
Nesse exercício iremos analisar a equação:
E descrever em palavras qual superfície a equação está descrevendo. Para isso vamos pensar nas coordenas cilíndricas , e . Se a gente entender o comportamento de cada uma dessas variáveis podemos imaginar o sólido descrito.
Vamos lá!
Passo 2
A questão nos deu para que:
Mas não diz nada sobre ou . Então vamos imaginar que e assumem todos os valores possíveis.
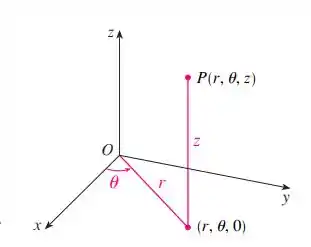
A imagem traz um exemplo da localização de uma coordenada cilíndrica no espaço. Vemos ali que é um ângulo no plano medido em relação ao eixo .
Olhando os valores de , como o exercício não trouxe informação nem restrições sobre ela assume todos os valores possíveis.
O mesmo acontece com , então vamos imaginar que nossa superfície tem extensão infinita na dimensão e em também.
Temos para as coordenadas cilíndricas a equação:
Então, teremos:
Calculando a tangente:
Então, podemos dizer que no plano essa superfície tem a equação:
Como temos que , mas não temos nenhuma restrição sobre e , a superfície é um plano incluindo o eixo e interceptando o plano na linha com inclinação .
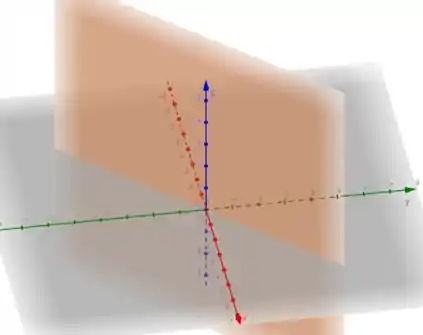
Resposta
a superfície é o plano incluindo o eixo e interceptando o plano na linha com inclinação