Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.8 - Ex. 7
Identifique a superfície cuja equação é dada.
Passo 1
Fala, pessoal!
Essa questão é bem simples. Ela pede pra gente identificar que superfície estamos trabalhando com essa equação aqui, ó:
Olha só, tanto em coordenadas cilíndricas como polares a gente sabe que
Mexendo na equação dada, a gente tem noção de qual será a superfície, show?
Passo 2
Substituindo na equação, teremos:
Isso indica que estamos em relação ao eixo , onde essa é a equação de um paraboloide que sai da altura e tem concavidade negativa.
Aqui está o esboço:
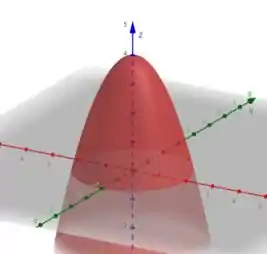
Show de bolinha! 😊
Resposta
A equação descreve um paraboloide
Exercícios de Livros Relacionados
Calcular ∭_T^() d V , onde T é a região limitada por x^2 + y^2 = 4 e y^2 + z^2 = 4 .
Calcular ∭ T z . d V , onde T é a região interior às superfícies z = - 1 4 ( x 2 + y 2 ) e x 2 + y 2 + z 2 = 5 .
Calcular ∭_T^() d V , onde T é a região limitada por x^2 + y^2 - x = 0 e x^2 + y^2 + z^2 = 1 .
Calcular ∭ T z . d V , onde T é a região interior às superfícies z = 1 4 ( x 2 + y 2 ) e x 2 + y 2 + z 2 = 5 .
Calcular ∭ T ( x 2 + y 2 ) d V , onde T é a região interior ao cilindro x 2 + y 2 = 1 e à esfera x 2 + y 2 + z 2 = 4 .