Descreva em palavras a superfície cuja equação é dada.
Passo 1
Oii, pessoal! Tudo certinho?
Nesse exercício iremos analisar a equação:
E descrever em palavras qual superfície a equação está descrevendo. Para isso vamos pensar nas coordenadas cilíndricas , e . Se a gente entender o comportamento de cada um dessas variáveis podemos imaginar o sólido descrito.
Passo 2
Sabemos das coordenadas cilíndricas que:
Então nesse caso, temos:
Ou seja, a equação está descrevendo um círculo de raio , no plano .
Como não foi especificada nenhuma condição com relação a e , eles podem assumir qualquer valor, então, imaginando todos os valores possíveis para essas variáveis:
E assim, acabam formando um cilindro ao redor do eixo com centro na origem e raio 5.
Como temos que , a distância de qualquer ponto dessa superfície está a uma distância de cinco unidades com relação ao eixo , ou seja, todos os pontos estão a uma distância constante do eixo , formando assim um cilindro.
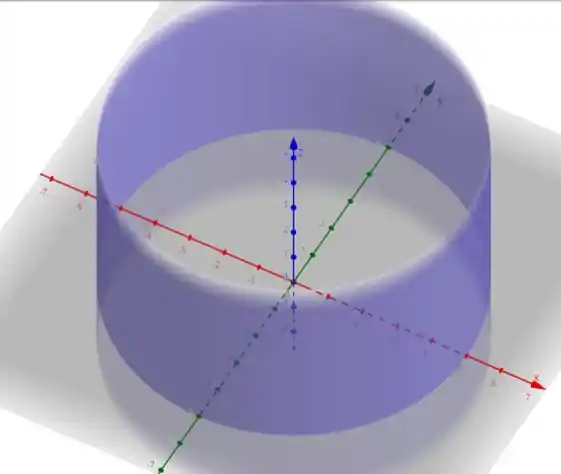
Resposta
Cilindro ao redor do eixo com centro na origem e raio 5.