Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.6 - Ex. 51
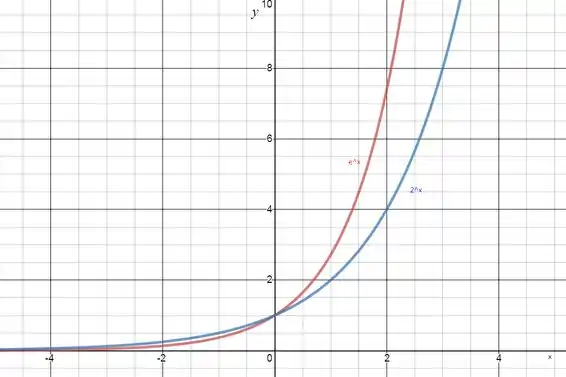
Faça esboços, no mesmo conjunto de eixos, dos gráficos de de e . Ache a área da região limitada pelos dois gráficos e pela reta .
Passo 1
O primeiro passo para o esboço de um gráfico é analisar seu domínio e imagem. Ambas as funções estão apenas definidas para e tem como imagem o conjunto .
Passo 2
O segundo passo é observar as assíntotas e quando as funções cruzam os eixos cartesianos. Podemos notar facilmente que:
Temos então para as duas funções uma assíntota em quando vai ficando muito pequeno. Além disso:
Então ambas as funções vem de próximo de 0 quando é pequeno, cruzam o eixo y em e vão para o infinito quando vai para o infinito. Agora basta analisarmos e compararmos os valores e como é o crescimento de cada uma.
Passo 3
Como , para valores positivos de teremos e para valores negativos de teremos .
Derivando as duas funções:
Podemos notar que para valores pequenos de teremos a derivada de maior, e para valres grandes a derivada de será maior. Agora que conseguimos comparar as duas funções e analisar o comportamento de cada uma, podemos esboçar os gráficos.
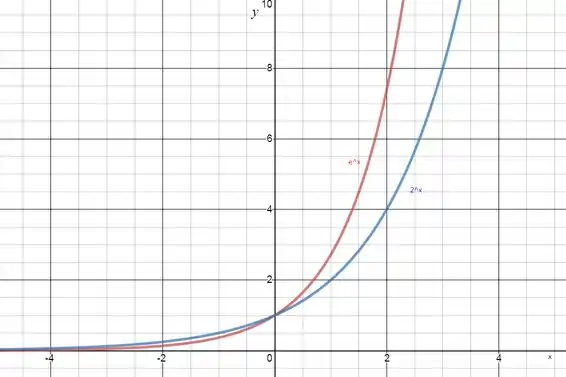
Passo 4
Para calcularmos a integral limitada pelas funções e a reta , percebemos primeiro que a região se inicia quando as duas funções se cruzam em , e que nessa parte do gráfico. A área então é calculada por:
Passo 5
Sabendo que e , calculamos a integral definida:
Resposta
