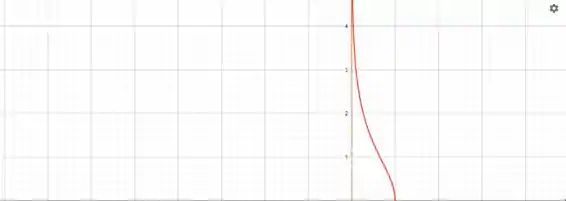
Faça um esbolo do gráfico da função:
A função inversa da secante hiperbólica
Passo 1
Não vamos gastar um milhão e meio de contas aqui.
Já temos na outra seção como fazer o gráfico da cotangente hiperbólica.
Ele vai ser:
Assíntotas horizontais:
O gráfico vai ficar:
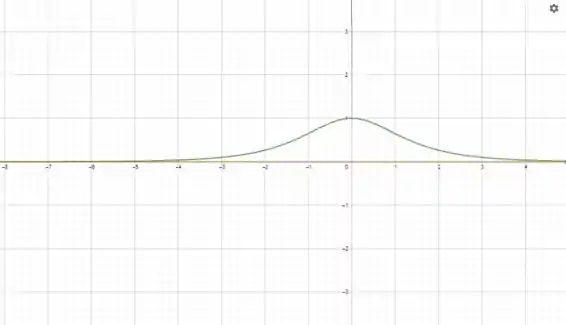
Como chegamos na inversa a partir dessa?
A ideia da inversa é trocar os eixos e de lugar. Para isso, vamos rodar o gráfico todo.
Temos que fazer movimentos:
Inverter o
Rodar graus no sentido anti-horário.
Passo 2
O primeiro movimento é Inverter o
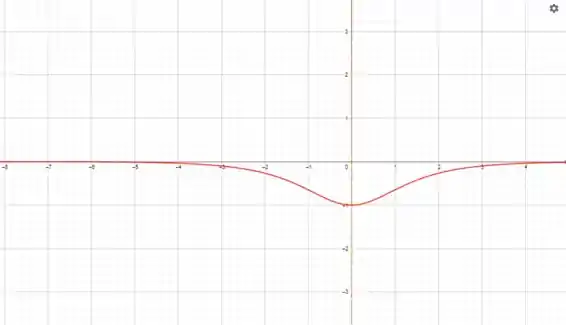
Passo 3
Rodar graus no sentido anti-horário.
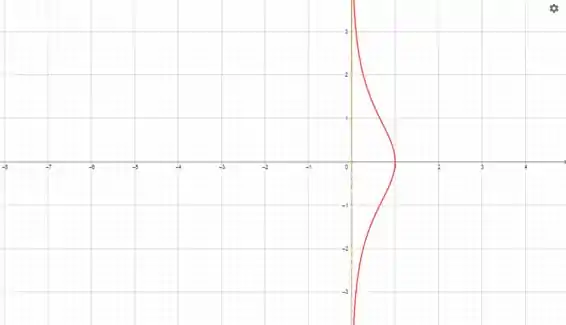
Calma, isso não é uma função. Não podemos ter dois valores de para um único de .
Vamos pegar só a parte de cima desse gráfico então:
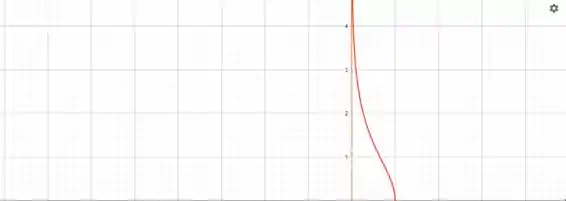
Resposta