Faça uma figura apropriada e descreva a ideia básica do Método de Newton, sem usar fórmulas.

O método de Newton busca aplicar sucessivamente uma “fórmula” a partir de um valor inicial, conhecido como método de aproximações sucessivas. Em outras palavras, dada uma função para qual desejamos encontrar uma raiz, escolhemos um valor inicial, e aplicamos uma fórmula a este valor repetidamente, assim achamos uma sequência de pontos que vai convergir a uma raiz da função.

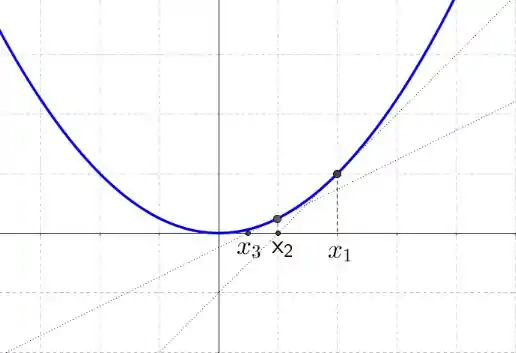
Vamos descrever através da figura abaixo, dado um valor inicial , achamos a reta tangente ao gráfico de nesse ponto, e definimos o número como sendo o ponto de interseção desta reta com o eixo , e vamos repetindo até que o valor convirja. Quando o valor converge, encontramos uma aproximação de uma raiz da função.