Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 38
Obtenha um gráfico da função e identifique a localização de todos os pontos críticos e de inflexão. Confira seu trabalho com um recurso gráfico.
Passo 1
Bom, galera, um ponto crítico é um ponto no domínio de uma função onde a primeira derivada é nula ou não é definida. Já o ponto de inflexão, é um ponto sobre uma curva na qual a curvatura troca o sinal.
Assim, precisamos calcularmos as derivadas da expressão:
Portanto, graficamente, temos um ponto crítico em e um ponto de inflexão em .
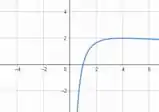
Prontinho!!
Resposta
ponto crítico em e ponto de inflexão em .
Exercícios de Livros Relacionados
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar