Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.2 - Ex. 33c
Faça o gráfico de no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ao esboço, dado que seja a extremidade esquerda, a extremidade direita e o ponto médio do -ésimo subintervalo. (Faça um esboço de cada subconjunto de retângulos.
Passo 1
O texto desta questão é bem confuso. Portanto, precisamos primeiro entender o que ela nos pede para fazer. Primeiramente, precisamos dividir um intervalo em quatro partes. Então, se temos e um , se queremos 4 subintervalos de comprimentos iguais, queremos descobrir os valores de , e tais que:
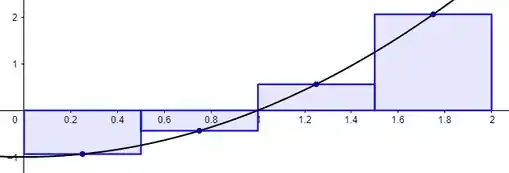
Descoberto os limites do intervalo, devemos expressar cada um dos retângulos referentes a esta partição utilizando o critério escolhido para o valor de (extremidade esquerda, direita ou ponto médio).
No final, a nossa questão pede apenas para esboçarmos o gráfico com os retângulos associados a soma de Riemann. Somente isto. Como ela é uma questão que utiliza recursos tecnológicos, não é necessário calcular o intervalo e os valores de e os valores de . Entretanto, será descrito aqui os passos iniciais para que isto seja feito manualmente.
Vamos então para a nossa questão!
Passo 2
Como o intervalo é , e queremos dividir em 4 subintervalos, o comprimento de cada intervalo é:
Consequentemente, a partição do nosso intervalo é:
Passo 3
Com esta partição, obtemos os seguintes intervalos:
Agora, se queremos analisar a partir do ponto médio, o valor de será obtido através da soma dos extremos dos intervalos dividido por 2, logo, o ponto intermediário.
Passo 4
Vamos agora obter o gráfico da nossa função expressando os retângulos associados a soma de Riemann.
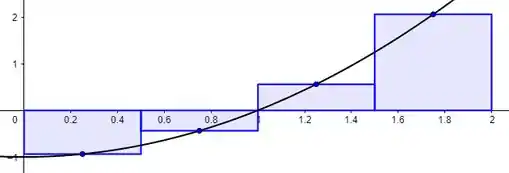
Resposta
