Faça o gráfico das duas soluções básicas da equação diferencial e de várias outras soluções. Que aspecto as soluções têm em comum?
Passo 1
Aqui temos uma equação diferencial linear de segunda ordem, da forma:
Vamos então achar a equação auxiliar:
Vamos manipular essa equação:
Temos que as raízes são e , portanto como as raízes são reais e destintas vamos usar a equação :
Temos que e são as soluções básicas, e temos o gráfico abaixo onde é a curva azul e a curva vermelha:
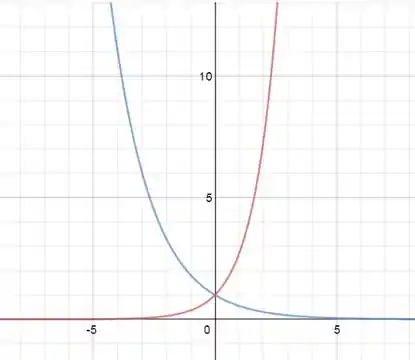
Vamos fazer agora de mais duas soluções:
Com sendo:
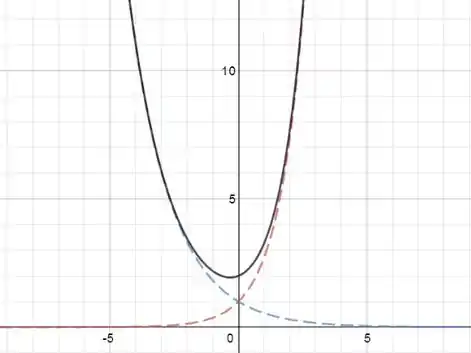
Com sendo:
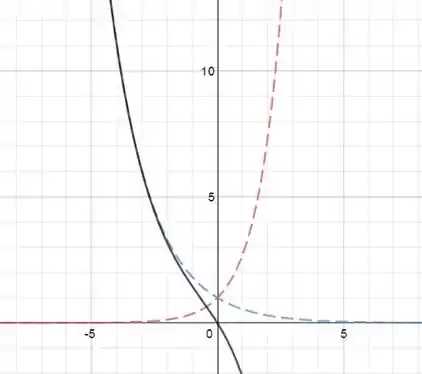
Elas tem em comum que todas são combinações lineares das soluções básicas.
Resposta
Gráfico da solução básica onde é a curva azul e a curva vermelha:
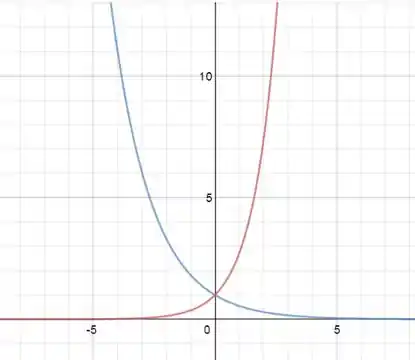
Com sendo:
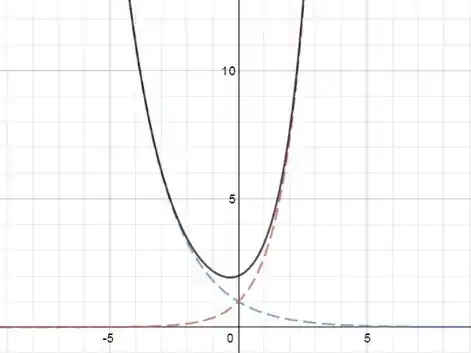
Com sendo:
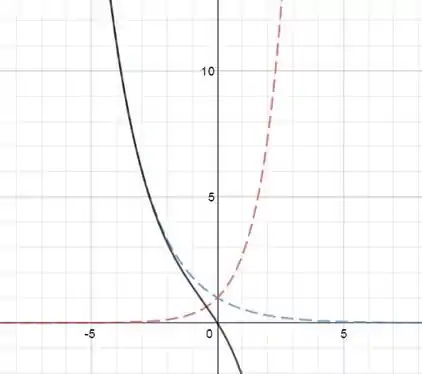
Elas tem em comum que todas são combinações lineares das soluções básicas.