Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 31
Determine o volume do sólido dado.
31.
Limitado pelo cilindro e pelos planos , , no primeiro octante.
Passo 1
Fala, galera!
A questão quer que a gente encontre o volume do sólido pela limitação do cilindro e pelos planos dados no primeiro quadrante, hein?
Show!
Olha só, o volume é definido por três planos (, beleza?
Quando , teremos um plano , que é definido pelo cilindro que nos foi dada na questão:
Vamos começar pegando nossa equação do cilindro e substituindo pelos planos, e assim acharemos nossos limites de integração no primeiro quadrante.
Passo 2
Quando , teremos:
Mas como queremos a região do primeiro quadrante, então no eixo nossa região será definida por:
Já quando
Então,
Graficamente, podemos representar assim:
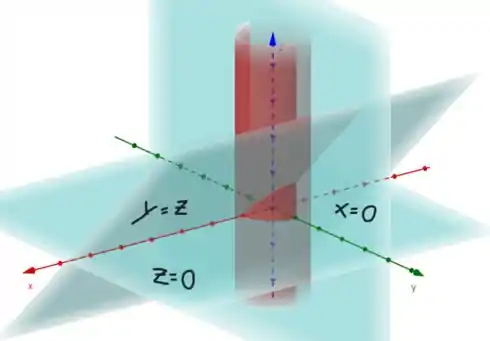
Mas como estamos de olho no primeiro quadrante, nosso plano será definido assim:
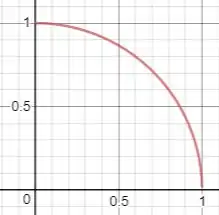
Nossa função pode ser representada por .
Assim, o volume será
Mas como , então
Passo 3
Calculando a integral de dentro, ou seja, em relação a :
Cancelando a raiz quadrada porque temos um expoente quadrado:
Beleza, agora resolvendo a integral em relação a , teremos:
Assim,