Faça o gráfico da função f x = sin ⁡ π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.

Fica impossível de verificarmos os valores de f x à medida que nos aproximamos da origem.

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 51

Faça o gráfico da função do Exemplo 4 na janela retangular por . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.

Passo 1

Eaee!!! Belezinha? Bom... primeiramente a questão quer que plotemos o gráfico da função na janela retangular por .

Em seguida, devemos aplicar um zoom diversas vezes em direção ao centro do gráfico e analisar o comportamento da função.

Mas antes de plotarmos, vamos pensar um pouquinho a respeito da nossa função?

Para isso, lembre-se que o seno é uma função varia de a .

😉

Passo 2

Então... a gente tem a seguinte função:

Perceba que, quanto mais aumentarmos o nosso valor de , o valor tenderá a zero. Assim, o seno tenderá para zero no infinito.

Agora, quanto mais diminuirmos o nosso valor de , maior será o valor de . Dessa forma, o limite no infinito irá divergir, ocasionando em uma indeterminação do seno em .

Agora vamos plotar utilizando um software matemático!

Passo 3

Plotando na janela por e dando o zoom em seguida, temos:

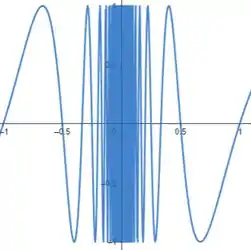
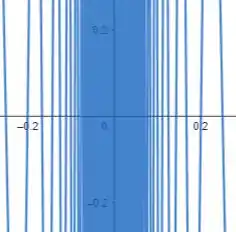
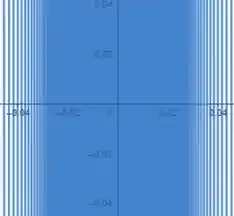
Perceba que fica impossível de verificarmos os valores de à medida que nos aproximamos da origem!!

Entendeu direitinho? Responde aee ;)

Resposta

Fica impossível de verificarmos os valores de à medida que nos aproximamos da origem.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma fórmula para uma função f que satisfaça as seguintes condições: lim x → ± ∞ ⁡ f x = 0;lim x → 0 ⁡ f x = - ∞ ; f 2 = 0; lim x → 3 + ⁡ f x = - ∞; lim x → 3 - ⁡ f x = ∞

Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = x 2 - x 6

Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = x 3 ⋅ x + 2 2 ⋅ ( x - 1 )

Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = x 2 ⋅ x 2 - 1 2 ⋅ ( x + 2 )

Seremos capazes de mostrar, no Capítulo 9 do Volume II, que, sob certas condições, a velocidade v ( t ) de uma gota de chuva caindo no instantet é v t = v * ( 1 - e - g t v * ) Encontre lim t → ∞ ⁡ v