Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 83

83.

a. Faça o gráfico de para estimar , aproximando-se da origem quando necessário.

b. Comfirme sua estimativa no item (a) com uma prova.

Passo 1

A gente precisa de algum software para desenhar esse gráfico, eu vou usar o GeoGebra, mas da para fazer com qualquer um.

Escrevendo a função nele vamos ter esse gráfico:

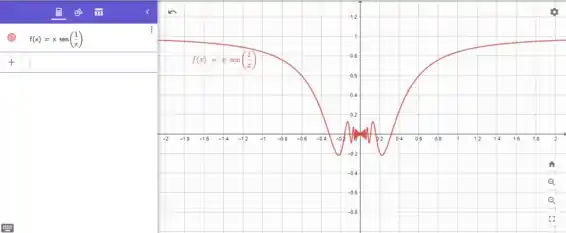
Para descobrirmos para onde esta tendendo o valor da função quando o tende a zero, vamo dar um zoom no e ver como a função se comporta:

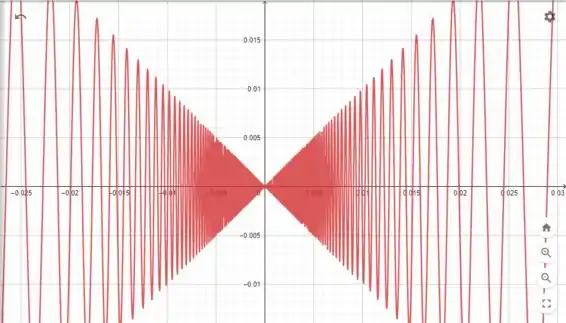
Podemos observar que quando menor o mais a função se aproxima de zero, então podemos estimar que

Passo 2

Para termos certeza, é só fazer o cálculo do limite:

A função seno é limita entre 0 e 1, ou seja, nunca vai ser maior do que 1 nem menor do que 0. Dessa forma, como tende a zero esse limite todo tende a 0.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule os limites justificando cada passagem pelas leis do limite que forem usadas. lim x → - 2 ⁡ ( 3 x 4 + 2 x 2 - x + 1 )

Calcule os limites justificando cada passagem pelas leis do limite que forem usadas. lim t → - 1 ⁡ t 2 + 1 3 ⋅ t + 3 5

Calcule os limites justificando cada passagem pelas leis do limite que forem usadas. lim x → 2 ⁡ 2 x 2 + 1 x 2 + 6 x - 4

Calcule os limites justificando cada passagem pelas leis do limite que forem usadas. lim x → 3 ⁡ x 2 - 4 ⋅ ( x 3 + 5 x - 2 )

Dado que lim x → a ⁡ f ( x ) = - 3 ,lim x → a ⁡ g x = 0 , lim x → a ⁡ h x = 8 Encontre, se existir, o limite. Caso não exista, explique por quê. lim x → a ⁡ f x + h x lim x → a ⁡ f x 2 lim x → a ⁡ h x