Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.6 - Ex. 53

(a) Faça uma substituição u apropriada da forma u = x 1 / n ou u = x + a 1 / n e, então, calcule a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao de (a).

∫ x x - 2   d x

Passo 1

(a) Faça uma substituição da forma u = x + a 1 / n .

Se :

u = x - 2 1 2

u 2 = x - 2

2 u d u = d x

x = u 2 + 2

Aplique a substituição.

∫ x x - 2   d x = ∫ u 2 + 2 u 2 u d u  

Multiplicando: ∫ x x - 2   d x = ∫ ( 2 u 4 + 4 u 2 ) d u

Para integral, vamos aplicar a fórmula que diz que:

∫ u n d u = u n + 1 n + 1 + C

Integrando:

∫ x x - 2   d x = 2 u 5 5 + 4 u 3 3 + C

Substituindo u = x - 2 1 2 :

∫ x x - 2   d x = 2 5 x - 2 5 / 2 + 4 3 x - 2 3 / 2 + C

Passo 2

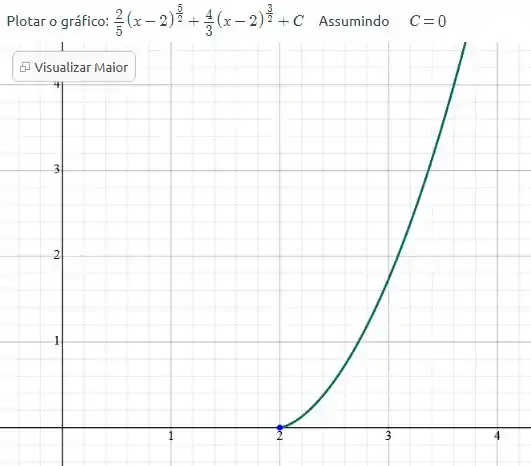
(b) Usando um CAS (pode ser até mesmo um programa online como é o caso do Symbolab):

Resposta

∫ x x - 2   d x = 2 5 x - 2 5 / 2 + 4 3 x - 2 3 / 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule.int_0^1 (1)/((x + 1)^5) d x
Calcule int_(- pi)^(pi) (sen x)/(x^4 + x^2 + 1) d x .
Suponha f contínua em [0,4] . Calcule int_(- 2)^2 x f (x^2) d x .
Calcule.int_0^2 e^(2 x) d x
Calcule.int_(- 2)^1 (3)/(4 + x) d x