Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 29
A faixa sombreada da figura a seguir foi cortada de uma esfera de raio por planos paralelos separados por unidades. Demonstre que a área de superfície da faixa é de .
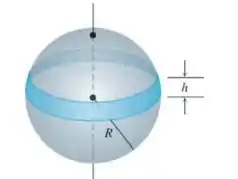
Passo 1
Para essa questão podemos calcular a área da curva (equação do círculo) em torno do eixo , considerando os limites de integração como , considerando , e assim dois pontos separados por unidades. A área da superfície gerada ao rotacionar a curva em torno do eixo é dada por:
Assim, temos que:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para x = y + 2 y , 1 ≤ y ≤ 2 ; eixo y :a) Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.b) Trace o gráfico da curva para ver como ela é. Se p
Para x = ∫ 0 y t gtd t ,0 ≤ y ≤ π 3 ; eixo y :Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.Trace o gráfico da curva para ver como ela é. Se
Para y = ∫ 1 x t 2 - 1d t ,1 ≤ x ≤ 5; eixo x :Estabeleça uma integral para a área da superfície gerada pela rotação da curva dada em torno do seu eixo.Trace o gráfico da curva para ver como ela é. Se
Determine a área da superfície lateral (lado) do cone gerado pela rotação do segmento de reta y = x 2 , 0 ≤ x ≤ 4 , em torno do eixo x . Verifique se sua resposta coincide com a fórmula geométrica.Áre
Determine a área da superfície lateral do cone gerado pela rotação do segmento de reta y = x 2,0 ≤ x ≤ 4 , em torono do eixo y . Verifique se seu resultado coincide com a fórmula geométrica: Á r e ad