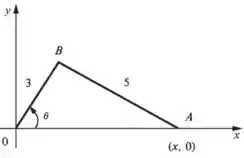
Suponha que os comprimentos dos segmentos e sejam, respectivamente, e . Suponha, ainda, que esteja variando a uma taxa constante de rad/s. Determine a velocidade de , quando rad.
Passo 1
Vemos que o ponto correrá sempre encostado no eixo , então, sua velocidade será dada pala variação de que é .
Assim, devemos relacionar com . Para isso, usamos a lei dos cossenos:
Derivando em relação a :
Passo 2
Quando rad, temos:
Quando o ângulo chegar a , o valor de será positivo, assim .
Se , e está variando a uma taxa constante de rad/s ( ), temos:
Logo, a velocidade de é de cm/s.
Resposta
A velocidade de é de cm/s.