Um fazendeiro quer cercar uma área de 1,5 milhão de pés quadrados em um campo retangular e então dividi-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerca?
Passo 1
Yuri aqui meu nobre amigo e estarei te ajudar a resolver essa atividade.
Em problemas de otimização como esse, devemos tentar representar a quantidade que queremos minimizar ou maximizar em função de um só parâmetro (nesse caso, a altura dos retângulos, por exemplo), para então analisar essa função e encontrar os extremos. A imagem mostra a divisão da área:
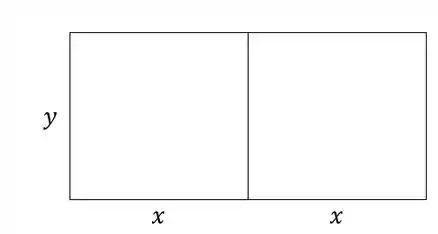
Vamos então tentar representar o custo da cerca em função da altura .
Passo 2
Primeiro vamos eliminar a variável , que é a largura de cada metade. Como a área é fixa em 1,5 milhões de pés quadrados, temos:
Sendo e representados em pés. O comprimento total da cerca é , então o custo da cerca pode ser representado por:
Se por o preço por pé. Colocando só em função de :
Passo 3
Agora temos o custo em função da altura , e devemos encontrar o mínimo dessa função. Para encontrarmos os pontos de máximo ou de mínimo de uma função, devemos derivar a equação da função e igualar a derivada a zero.
Como é uma distância, deve ser um número positivo, então vamos investigar a função para no intervalo . Podemos ter um ponto crítico se a derivada da função for zero ou não existir. Vamos derivar :
Como essa função sempre existe para , vamos investigar . Temos:
Repare que foi descartado pois deve ser positivo. Agora devemos verificar se em temos um valor mínimo. Se , podemos ver que é negativo, então a função é decrescente. Se , é positivo e então a função é crescente. Como a função é decrescente antes e crescente depois de , temos aí um ponto mínimo.
Passo 4
Sabemos que é um ponto mínimo, mas agora devemos saber se é o mínimo absoluto. Como esse é o único ponto crítico, agora basta olhar a função nos extremos do intervalo. Devemos então olhar os casos em que e que :
Como a função vai a mais infinito nos extremos do intervalo e é o único ponto mínimo local, é o ponto mínimo absoluto. Vamos então calcular também o valor de :
Resposta
Altura de 1000 pés, largura de 1500 pés dividida ao meio.