Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 103
A figura a seguir mostra uma parte do gráfico de uma função duas vezes derivável . Em cada um dos cinco pontos marcados, classifique e como positiva, negativa ou nula.
Passo 1
Sabemos que:
- se a função é crescente em x.
- se a função é decrescente em x.
- se x é um ponto crítico no gráfico (máximo ou mínimo absolutos)
- se a concavidade do gráfico é para cima em x.
- se a concavidade do gráfico é para baixo em x.
- se x é um ponto de inflexão (onde muda a concavidade)
Diante disso, podemos definir o sinal nos pontos...
Passo 2
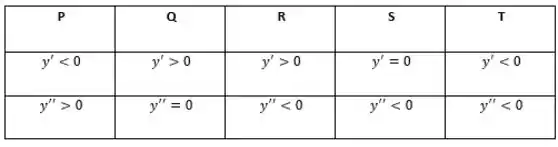
- Em P, a função é decrescente e a concavidade é para cima.
- Em Q a função é crescente, e Q é um ponto de inflexão.
- Em R, a função é crescente e a concavidade é para baixo.
- S é um ponto de máximo e a concavidade é para baixo.
- Em T a função é decrescente, e a concavidade é para baixo.
Com isso, temos que:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar
Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar