Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.5 - Ex. 26

A figura abaixo mostra uma calota esférica de altura h , cortada de uma esfera de raio r . Mostre que a área da superfície S da calota é S = 2 π r h . [Sugestão: Faça uma parte apropriada do círculo x 2 + y 2 = r 2 girar em torno do eixo y .

Passo 1

Precisamos usar essa fórmula aqui para provar que a área da superfície de da calota é é S = 2 π r h :

S = ∫ a b 2 π f x 1 + f ' x 2 d x

E o enunciado já dá um bizu para gente: podemos girar uma parte do círculo em torno de y . E como vamos girar em torno de y , precisamos fazer umas modificações na fórmula (só trocar x e y de lugar):

S = ∫ c d 2 π g y 1 + g ' y 2 d y

Vamos começar!

Passo 2

Que parte do círculo pode nos ajudar? Se vamos girar em torno de y , precisamos isolar x na equação do círculo para achar g ( y ) :

x 2 + y 2 = r 2 ∴ y = ± r 2 - y 2

Podemos usar o semicírculo na parte positiva de x :

g y = r 2 - y 2

Agora precisamos achar os extremos de integração. Repara no nosso desenho:

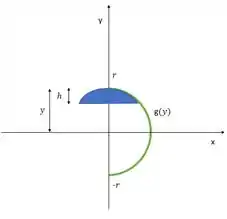
Em azul é a calota. Repara que a parte de g ( y ) que tem a calota está entre y = r - h e y = r . Então esses são os nossos extremos.

Passo 3

Sabemos que:

g y = r 2 - y 2

Precisamos calcular a derivada dela, usando a regra da cadeia:

g ' y = - 2 y ⋅ 1 2 r 2 - y 2

Passo 4

Vamos substituir tudo na nossa fórmula:

S = ∫ c d 2 π g y 1 + g ' y 2 d y

S = ∫ r - h r 2 π r 2 - y 2 1 + - 2 y ⋅ 1 2 r 2 - y 2 2 d y

Agora é integrar! Elevando nossa derivada ao quadrado e jogando nossa g ( y ) para dentro da raiz, depois fazendo a distributiva e rearrumando, ficamos com isso:

S = 2 π ∫ r - h r r 2 - y 2 + y 2 d y = 2 π ∫ r - h r r d y = 2 π r 2 - r 2 + r h

S = 2 π r h

Uhul! Conseguimos!

Resposta

Prova desenvolvida nos passos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Eis um desenho esquemático da redoma de 90 pés usada pelo Serviço Nacional de Meteorologia dos Estados Unidos para abrigar um radar em Bozeman, Montana.Qual é a área da superfície externa a ser pintad
Suponha que f seja lisa em [ a , b ] e dividida [ a , b ] da maneira usual. No k - é s i m o é subintervalo [ x k - 1 ,x k ] , construa a reta tangente à curva no ponto médio m k = x k - 1 + x k 2 , c
Determine a área da superfície gerada pela rotação do eixo x do pedaço de astroide x 2 3 + y 2 3 = 1 mostrado na figura a seguir. (Sugestão: gire o pedaço do primeiro quadrante y = 1 - x 2 3 3 2 ,0 ≤
Nos Exercícios 21-24, determine as áreas de superfícies geradas pela rotação das curvas em torno dos eixos dados.21. y = 2 x + 1 , 0 ≤ x ≤ 3 ; e i x ox
Nos Exercícios 21-24, determine as áreas de superfícies geradas pela rotação das curvas em torno dos eixos dados.24. x = y, 2 ≤ y ≤ 6 ; e i x oy