Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 54

Use a definição de derivada para encontrar f ' x e   f ' ' ( x ) . A seguir, trace f ,   f ' e   f ' ' , e em uma mesma tela e verifique se suas respostas são razoáveis.

f x = x 3 - 3 x

Passo 1

Vamos calcular a derivada primeira...

Pela definição de derivada, temos

f ' x =   lim h → 0 ⁡ f x + h - f ( x ) h

Vamos trazer isso pro nosso caso agora, substituindo a função...

f ' x = lim h → 0 ⁡ ( x + h ) 3 - 3 ( x + h ) - ( x 3 - 3 x )   h

f ' x = lim h → 0 ⁡ x 3 + x 2 h + 2 x 2 h + 2 x h 2 + h 2 x + h 3 - 3 x - 3 h - x 3 + 3 x h

f ' x = lim h → 0 ⁡ x 3 + x 2 h + 2 x 2 h + 2 x h 2 + h 2 x + h 3 - 3 x - 3 h - x 3 + 3 x h

f ' x = lim h → 0 ⁡ x 2 h + 2 x 2 h + 2 x h 2 + h 2 x + h 3 - 3 h h

f ' x = lim h → 0 ⁡ x 2 + 2 x 2 + 2 x h + h 2 - 3

f ' x = 3 x 2 - 3

Vamos para a derivada segunda agora...

Passo 2

Vamos aplicar a definição de derivada em f ' x e encontrar f ' ' x …

f ' ' x = lim h → 0 ⁡ 3 x + h 2 - 3 - ( 3 x 2 - 3 ) h

f ' ' x = lim h → 0 ⁡ 3 x 2 + 6 x h + 3 h 2 - 3 - 3 x 2 + 3 h

f ' ' x = lim h → 0 ⁡ 6 x h + 3 h 2 h

f ' ' x = lim h → 0 ⁡ 6 x + 3 h

f ' ' x = 6 x

Prontinho! Agora só falta a gente ver pelos gráficos se encontramos soluções razoáveis...

Passo 3

Vamos ver...

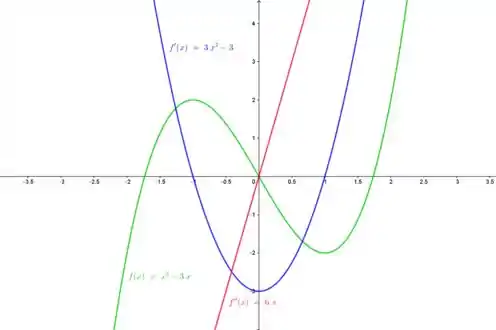
Olha só, quando a função f ' corta o eixo x, a função f tem uma reta tangente horizontal.

Quando f ' é negativa, f é decrescente, quando f ' é positiva, f   é crescente.

E quando f ' ' é negativa, a concavidade de f é para baixo, quando f ' ' é positiva, a concavidade de f é para cima...

Então, são soluções razoáveis (e corretas!)😉

Resposta

f ' x = 3 x 2 - 3

f ' ' x = 6 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos Exercícios de 51 a 54, ache a derivada da função dada. (Sugestão: |a| = a 2 ) 53 .g x = | x | 3
Nos exercícios de 51 a 54, ache a derivada da função dada. (Sugestão: | a | = a 2 )52. g x = x | x |