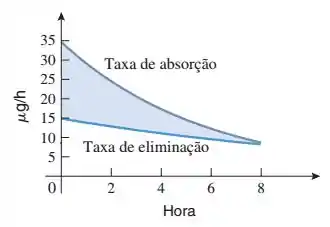
A figura abaixo mostra as taxas segundo as quais um medicamento é absorvido e eliminado pela corrente sanguínea de um indivíduo. Ambas as taxas são dadas em unidades de microgramas por hora () e exibidas num período de 8 horas. O que representa a área entre as curvas acima do intervalo ? Justifique sua resposta.

Vamos pensar aqui. Podemos escrever a taxa de absorção como:

Com em horas. E a taxa de eliminação como:

Porque elas são taxas de variação de uma grandeza ao longo do tempo, ou seja, derivadas.

A gente pode escrever essa área assim:

Mas a gente sabe que quando integramos uma derivada, voltamos a função inicial:

Repara que é o saldo de absorção de medicação que na corrente sanguínea em um instante. Quando a gente diminui esse valor entre dois instantes, estamos verificando a variação de absorção de medicamento na corrente sanguínea entre de uma hora para outra. Logo a área é igual à variação na quantidade de medicamento na corrente sanguínea entre e horas.