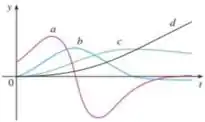
4. A figura mostra os gráficos de quatro funções. Uma é a função posição de um carro, a outra, a velocidade do carro, uma terceira, a aceleração e uma quarta, o arranco. Identifique cada curva e explique sua escolha.
Passo 1
E aí! tudo certinho?
Nesse problema foram dados quatro gráficos e nosso objetivo é determinar qual representa a posição de um carro, qual representa a velocidade desse carro, qual representa a aceleração e qual representa seu arranco.
Parece complicado?
O gráfico que foi dado é
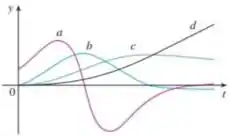
Da física nós sabemos que se é a função posição
Onde e são as funções velocidade e aceleração respectivamente.
O arranco é o quanto de aceleração que você ganha por tempo ou seja:
Ou seja, quando derivamos o espaço em relação ao tempo, obtemos a velocidade, quando derivamos mais uma vez obtemos a aceleração e derivando uma terceira vez, obtemos o arranco.
Então temos que descobrir quais funções são suas derivadas e relacionar com os princípios físicos que vimos anteriormente.
Saca só!
Passo 2
Tem duas coisas que podemos analisar para descobrir rapidamente qual função é derivada de qual:
- Na coordenada em que uma função atinge seu mínimo ou máximo local a derivada cruza o zero.
- Quando uma função está decrescendo sua derivada é negativa e quando ela está crescendo a derivada é positiva.
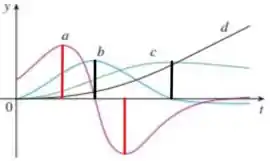
Perceba que não possui nenhuma derivada, já que quando ela está em seus pontos de máximo ou mínimo, nenhuma outra função corta o eixo , assim já podemos dizer que pois nas relações do passo 1, o arranco foi a única função que não tinha derivada.
Podemos observar tambem que quando atinge seu máximo é a única função que está em zero. Logo, a função é derivada da função ⇒
Quando a função atinge seu máximo a única função que está em zero é . Ou seja
A função só cresce então sua derivada precisa ser toda positiva, a única função que apresenta essa característica é a função . Então ⇒
Então quando derivamos obtemos , derivando pela segunda vez obtemos , derivando mais uma vez obtemos , com isso podemos escrever que:
E então! O que achou? Responde Aí!