Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.1 - Ex. 16
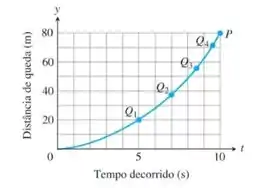
A figura a seguir mostra o gráfico da distância em função do tempo da queda de um objeto que caiu do módulo lunar a uma distância de da superfície da Lua.
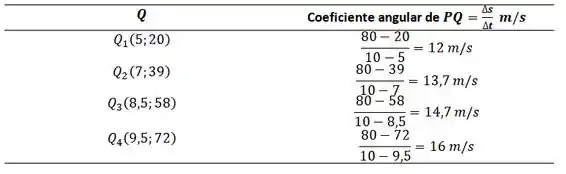
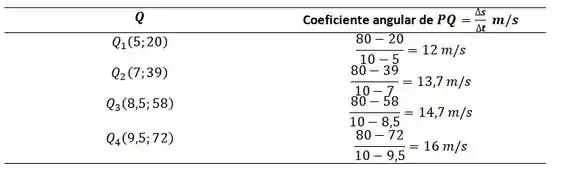
- Estime os coeficientes angulares das secantes , , e , arranjando-os em uma tabela, como mostra a Figura 2.6.
- Qual a velocidade aproximada do objeto ao cair na superfície?
Passo 1
A primeira coisa que precisamos fazer é lembrar que o coeficiente angular é calculado pela diferença da distância sobre o tempo decorrido:
Assim,
Passo 2
Como o coeficiente angular da função espaço é , então o coeficiente angular é a velocidade do objeto, portanto ao cair na superfície ():
Resposta
Exercícios de Livros Relacionados
7-Faça o gráfico de Determine lim x → 1 - f ( x ) e lim x → 1 + f ( x ) .Existe lim x → 1 f ( x ) ? Em caso afirmativo, qual é? Em caso negativo, por que não?
Quais afirmações a seguir sobre a função y = f ( x ) representadas no gráfico são verdadeiras e quais são falsas? lim x → - 1 + f x = 1 b) lim x → 0 - f x = 0 c) lim x → 0 - f x = 1 d) lim x → 0
Seja g x = xs e n 1 x Determine lim x → 0 + g ( x ) Em caso afirmativo, qual é? Em caso negativo por que não?Determine lim x → 0 - g ( x ) Em caso afirmativo, qual é? Em caso negativo por que não?
Quais afirmações a seguir sobre a função y = f ( x ) representadas no gráfico são verdadeiras e quais são falsas? lim x → - 1 + f x = 1 b) lim x → 2 f xn a oe x i s t e c) lim x → 2 f x = 2 d) l
Seja Determine lim x → 2 + f ( x ) e lim x → 2 - f ( x ) e f ( 2 ) .Existe lim x → 2 f ( x ) ? Em caso afirmativo, qual é? Em caso negativo por que não?Determine lim x → - 1 - f ( x ) e lim x