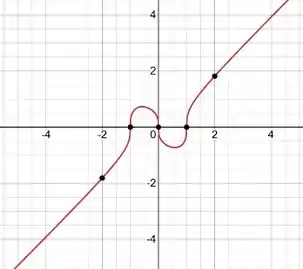
Esboce o gráfico.
Passo 1
Oi, pessoal! Tudo bom? Antes de começar a esboçar qualquer gráfico é importante a gente saber qual o domínio dele.
Repara que é uma raiz é cúbica e não quadrada, ou seja, não tem problema seu interior ser negativo, logo
Como não existe um ponto que dê problema na função, não vamos ter candidatos a assíntotas verticais.
Então agora vamos verificar se há assíntotas horizontais calculando os limites e depois derivar para avaliar as concavidades!
Passo 2
Pras horizontais no entanto, analisamos o resultado dos limites:
Colocando em evidência,
Agora vamos escrever o limite como um produto
Repara que o segundo limite vai ser igual a
Por fim:
Belê, sem assíntotas horizontais também já que esses limites deram infinitos
Passo 3
Vamos usar a regra da cadeia! Então temos que,
Lembrando que a derivada do polinômio e da função constante são:
Vamos então aplicar:
E logo:
Agora vamos analisar os sinais!
Passo 4
Os intervalos de crescimento e decrescimento são os intervalos em que, respectivamente, a primeira derivada é positiva e negativa. Veja que o denominador vai ser sempre positivo por causa do termo ao quadrado, então vamos analisar o numerador:
Analisando intervalos que contenham essas raízes e que contenham e também já que a primeira derivada não está definida nesse ponto, temos:
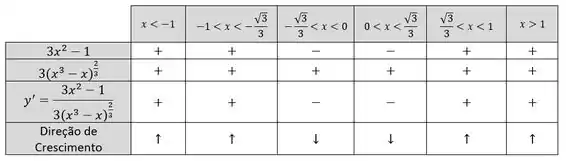
A setinha para cima indica que a função cresce e para baixo que ela descreve naquele intervalo
Passo 5
Vamos achar os pontos de inflexão e como se comporta a concavidade através de usando mais uma regra, a da divisão:
Seja
Vamos ter:
E também:
Aplicando:
Dividindo em cima e em baixo por
Note que:
Sempre, ou seja, quem dita o sinal da segunda derivada é o denominador. Como o denominador é bem parecido com o denominador da primeira derivada, podemos analisar o sinal da segunda derivada nos mesmos pontos da outra vez: , e . Bora:
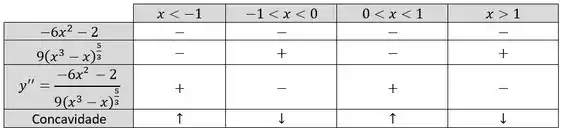
OBS: Como o numerador é sempre negativo, não vão existir pontos de inflexão pois nenhum ponto faz a segunda derivada zerar.
Passo 6
Pronto, agora podemos esboçar o gráfico, ficando desse jeito:
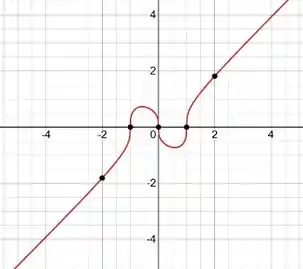
Resposta