Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 63

Uma folha de papelão quadrada com 12 cm de lado é usada para fazer uma caixa sem tampa cortando quadrados de tamanho igual dos quarto cantos e dobrando para cima os lados. Qual o tamanho dos quadrados que devem ser cortados fora para se obter uma caixa de maior volume possível?

Passo 1

Vamos analisar os dados do enunciado, temos a figura abaixo, que mostra o tamanho dos quadrados que devem ser cortados fora de lado x , o comprimento do lado todo de 120 :

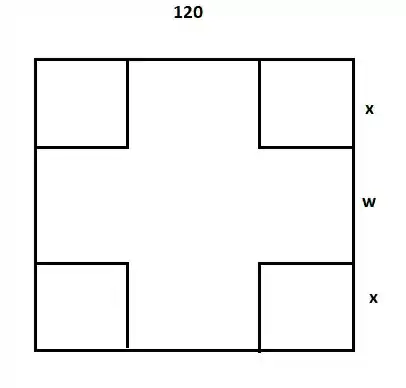
Temos então a expressão:

2 x + w = 12

E temos também a expressão do volume:

V = x ⋅ w ⋅ w = x w 2

Passo 2

Vamos agora isolar w da primeira expressão e substituir na do volume:

2 x + w = 12 → w = 12 - 2 x

Substituindo:

f x = x w 2 = x 12 0 - 2 x 2 = x 14 4 00 - 480 x + 4 x 2 = 14 4 00 x - 480 x 2 + 4 x 3

Agora para obter um maior volume possível vamos derivar a expressão e igualar a zero para os pontos críticos, que são os possíveis valores:

f ' x = 14400 - 480 ⋅ 2 ⋅ x 2 - 1 + 4 ⋅ 3 ⋅ x 3 - 1 = 14 4 00 - 960 x + 12 x 2 = 0

14 4 00 - 960 x + 12 x 2 = 0 →

x = 60

x = 20

Passo 3

Temos então que os pontos críticos são 20 e 60 , temos que avaliar o f desses pontos:

f 20 = 14400 ⋅ 20 - 480 ⋅ 20 2 + 4 ⋅ 20 3 = 128000

f 60 = 14400 ⋅ 6 0 - 480 ⋅ 6 0 2 + 4 ⋅ 6 0 3 = 0

Pronto, temos que x = 20 é o tamanho dos quadrados que devem ser cortados fora para se obter uma caixa de maior volume possível.

Resposta

x = 2 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 1 a 22 encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f x = 7 ( a x 2 + b x + c
Nos exercícios 1 a 22 encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f x = 14 - 1 2 x - 3
Nos exercícios 1 a 22 encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f x = 3 x 2 + 6 x - 10
Nos exercícios 1 a 22 encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f u = ( 4 u 2 - a ) ( a -
Nos exercícios 1 a 22 encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico. f r = π r 2