Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.4 - Ex. 66
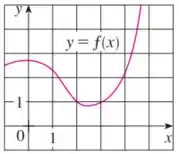
Se for a função cujo gráfico está mostrado, seja e . Use o gráfico de para estimar o valor de cada uma das derivadas.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico de :
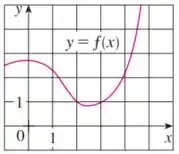
O enunciado ainda nos dá duas funções:
E
Com base nesse gráfico, queremos encontrar as seguintes derivadas em seus respectivos pontos:
e
Perceba que tanto a função , quanto a função são funções compostas, pois temos uma função dentro da outra. Sendo assim, para resolver essa questão podemos apenas pegar a definição da regra da cadeia, onde temos que se:
E sua derivada será dada pela relação
Ou seja, a derivada da função de dentro multiplicada pela derivada da função de fora.
Agora bora lá!! 😉
Passo 2
- Assim, como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
- Assim, como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Vamos olhar no gráfico o valor de , assim achamos que:
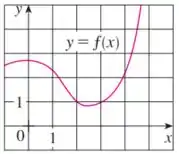
Veja que no ponto a função assume valor igual a . Então podemos escrever:
Passo 3
Agora para achar as derivadas nos pontos pedidos vamos ter que achar dois pontos que engoblem o valor pedido que sejam lineares de cada função, vamos lá:
Para temos os pontos e , assim, temos que a inclinação é:
Para temos os pontos e , assim, temos que a inclinação é:
Agora é só substituir de volta:
Passo 4
Derivando a parte final, ficamos com:
E substituindo o por , temos:
Passo 3
Para temos os pontos e , assim, temos que a inclinação é:
Agora é só substituir de volta:
E prontinho, tudo calculado.