Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.6 - Ex. 98

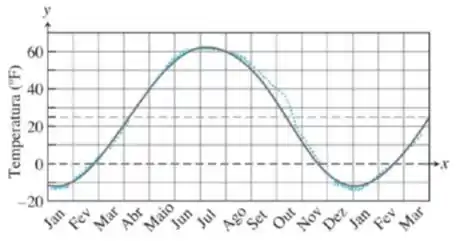
Temperaturas em Fairbanks, Alaska. O gráfico a seguir mostra a temperatura média em Fahrenheit em Fairbanks, Alaska, durante um ano típico de 365 dias. A equação que fornece a temperatura aproximada no dia x é

y = 37   s e n 2 π 365 x - 101 + 25

E é representada na figura a seguir.

  1. Em que dia a temperatura aumenta mais rapidamente?
  2. Quantos graus por dia, aproximadamente, a temperatura sobe quando aumenta mais rapidamente?

Passo 1

A questão nos pergunta duas informações. Para resolvermos a letra b ) , precisamos obrigatoriamente resolver a letra a ) , pois precisamos saber qual o dia em que a temperatura sobe mais rapidamente. Mas aí temos um questionamento, como vamos descobrir este dia? Observem que a letra a ) nos faz uma pergunta de taxa de crescimento. Quando esta taxa será máxima? E o que relacionamos a taxa de variação??? Sim! Isto mesmo! A derivada de uma função. Basta maximizarmos a nossa derivada!

Agora que descobrimos o dia, podemos ir para a letra b ) . É só obter o valor da taxa de variação neste dia. Simples, não é?

Passo 2

Vamos começar derivando a função temperatura. Desta forma, temos:

y ' = 37   s e n 2 π 365 x - 101 + 25 '

y ' = 37 ⋅ s e n 2 π 365 x - 101 '

y ' = 37 ⋅ cos ⁡ 2 π 365 x - 101 ⋅ 2 π 365 x - 101 '

y ' = 37 ⋅ cos ⁡ 2 π 365 x - 101 ⋅ 2 π 365

y ' = 74 π 365 cos ⁡ 2 π 365 x - 101

Passo 3

A taxa de variação da temperatura será máxima quando y ' for máximo. Isto vai ocorrer quando cos ⁡ 2 π 365 x - 101 for máximo, igual a 1. Desta forma, para que o cosseno seja igual a 1, x deve ser igual a 101 , isto é, em 11 de Abril.

cos ⁡ 2 π 365 101 - 101 = cos ⁡ 2 π 365 ⋅ 0 = cos ⁡ 0 = 1

Passo 4

Agora que descobrirmos o valor de x que maximiza a taxa de variação da temperatura, para descobrirmos quantos graus a temperatura sobe neste dia, basta substituirmos x = 101 na equação de y ' . Assim, temos:

y ' = 74 π 365 cos ⁡ 0

y ' = 74 π 365 ≅ 0,637   ° F

Resposta

  1. Quando x = 101 , no dia 11 de Abril.
  2. 0,637   ° F .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 51-70, determine (d y)/(d t) . 67. y = t g^2 ( s e n^3 t )
Nos Exercícios 51-70, determine (d y)/(d t) . 56. y = ( t^(- (3)/(4)) . s e n t )^((4)/(3))
Nos Exercícios 51-70, determine (d y)/(d t) . 64. y = (1)/(6) . (1 + c o s^2 (7 t)) ³ ³
Nos Exercícios 51-70, determine (d y)/(d t) . 62. y = cos ( 5 s e n ((t)/(3)) )
Nos Exercícios 51-70, determine (d y)/(d t) . 68. y = c o s^4 ( s e c^2 (3 t) )